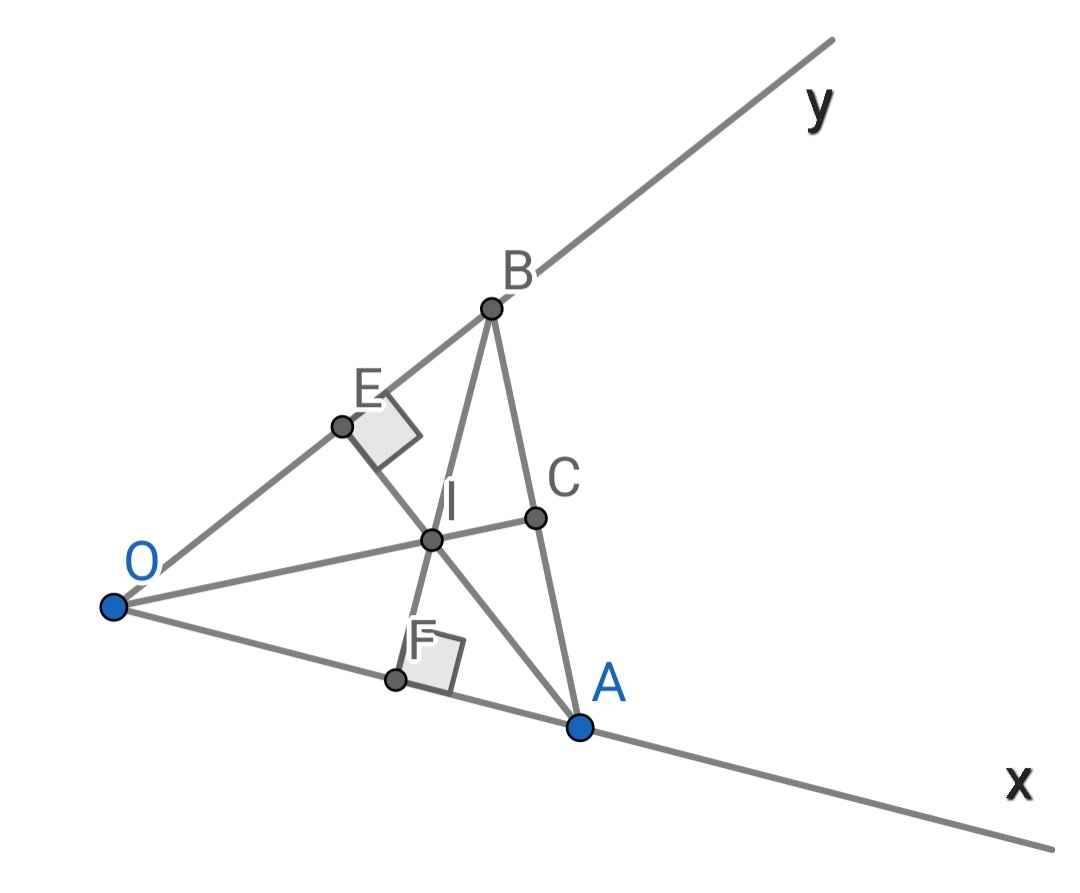
 a) Xét hai tam giác vuông: ∆OAE và ∆OBF có:
a) Xét hai tam giác vuông: ∆OAE và ∆OBF có:
OA = OB (gt)
∠O là góc chung
⇒ ∆OAE = ∆OBF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng)
b) Do OE = OF (cmt)
OB = OA (gt)
⇒ BE = OB - OE
= OA - OF
= AF
Xét hai tam giác vuông: ∆BAE và ∆ABF có:
AB là cạnh chung
BE = AF (cmt)
⇒ ∆BAE = ∆ABF (cạnh huyền - cạnh góc vuông)
⇒ ∠BAE = ∠ABF (hai góc tương ứng)
c) Gọi C là giao điểm của OI và AB
Xét hai tam giác vuông: ∆OIE và ∆OIF có:
OE = OF (cmt)
OI là cạnh chung
⇒ ∆OIE = ∆OIF (cạnh huyền - cạnh góc vuông)
⇒ ∠IOE = ∠IOF (hai góc tương ứng)
⇒ ∠COB = ∠COA
Xét ∆OAC và ∆OBC có:
OC là cạnh chung
∠COA = ∠COB (cmt)
OA = OB (gt)
⇒ ∆OAC = ∆OBC (c-g-c)
⇒ ∠OCA = ∠OCB (hai góc tương ứng)
Mà ∠OCA + ∠OCB = 180⁰ (kề bù)
⇒ ∠OCA = ∠OCB = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AB
⇒ OI ⊥ AB


