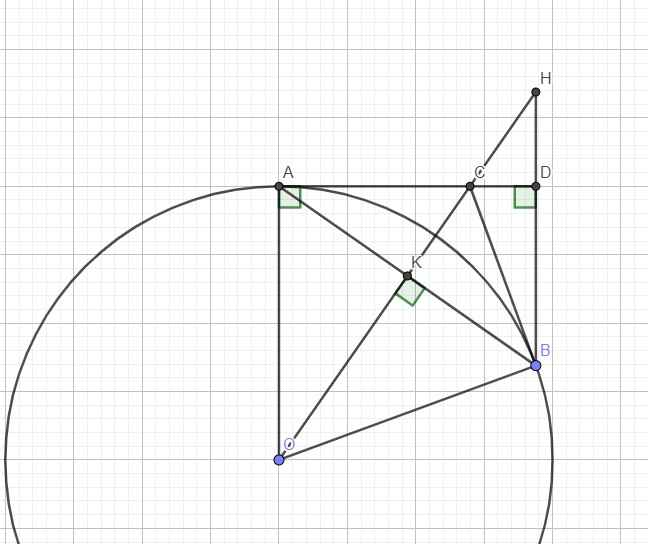
Theo tính chất 2 tiếp tuyến cắt nhau ta có \(AC=BC\)
Mặt khác \(OA=OB=R\)
\(\Rightarrow OC\) là trung trực AB hay \(OC\perp AB\)
\(\Rightarrow\Delta AOK\) vuông tại K
\(\Rightarrow\) Tập hợp K là đường tròn (C) đường kính AO cố định
b.
Do H là trực tâm \(\Rightarrow BH\perp AD\Rightarrow BH||AO\) (cùng vuông góc AD)
\(\Rightarrow\widehat{OAK}=\widehat{KBH}\) (so le trong)
Mà \(AK=BK\) (OC là trung trực AB)
\(\Rightarrow\Delta_VOAK=\Delta_VKBH\left(g.c.g\right)\)
\(\Rightarrow OK=KH\) hay K là trung điểm OH
\(\Rightarrow\overrightarrow{OH}=2\overrightarrow{OK}\Rightarrow H\) là ảnh của K qua phép vị tự tâm O tỉ số \(k=2\)
\(\Rightarrow\) Tập hợp H là đường tròn ảnh của (C) qua phép vị tự tâm O tỉ số \(k=2\) (với (C) là đường tròn đã xác định ở câu a)