Question

Cho đường tròn (O; R) và điểm S cố định nằm ngoài đường tròn (O). Kẻ hai tiếp tuyến SA và SB của đường tròn (O; R)(A, B là tiếp điểm). Đường thẳng bất kỳ qua S cắt đường tròn (O) tại C và D(SC < SD và C, O, D không thẳng hàng). Gọi E là trung điểm của đoạn thẳng CD. 1 Chứng minh bốn điểm S, A, 0, B cùng thuộc một đường tròn.

Mik cần hình và phần giải câu a 

Answer 1

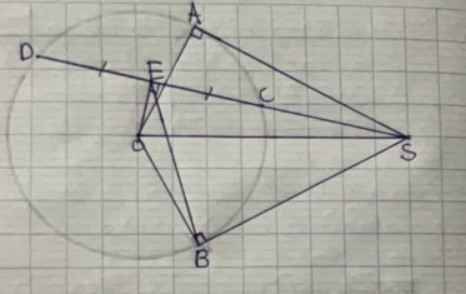
Xét tứ giác SOAB có: \(\left\{{}\begin{matrix}\widehat{SAO}=90^o\\\widehat{SBO}=90^o\end{matrix}\right.\)

=> Tứ giác SOAB nội tiếp (tổng 2 góc đối = 180^o).

=> 4 điểm S, A, O, B cùng thuộc 1 đường tròn.

Answer 2

góc SAO+góc SBO=180 độ

=>SAOB nội tiếp