Cho ΔABC , đường cao AH với H thuộc BC và AB<AC . Gọi hình chiếu của H lên các đoạn thẳng AB AC , lần lượt là M và N.
a) Chứng minh ΔAHM ~ ΔABH . Từ đó chứng minh AH^2= AM.AB .
b) Chứng minh AM.AB=AN.AC . Từ đó chứng minh ΔAMN~ΔACB .
c) Giả sử ΔABC vuông tại A và AB=6cm và AC=8cm . Tính tỷ số diện tích của tứ giác BMNC và ΔABC
d) Chứng minh 4 đường trung trực của các đoạn thẳng BM,MN,NC,CB đồng quy tại một điểm.
tui còn mỗi câu c và d thôi ai giúp với
c) Vì tam giác ABC vuông tại A \(\Rightarrow AMHN\) là hình chữ nhật
Ta có: \(\dfrac{S_{BMNC}}{S_{ABC}}=\dfrac{S_{ABC}-S_{AMN}}{S_{ABC}}=1-\dfrac{S_{AMN}}{S_{ABC}}\)
Ta có: \(\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AM.AN}{\dfrac{1}{2}.AB.AC}=\dfrac{AM.AN}{AB.AC}=\dfrac{AM.AB.AN.AC}{\left(AB.AC\right)^2}\)
\(=\dfrac{AH^2.AH^2}{\left(AH.BC\right)^2}=\dfrac{AH^4}{\left(AH.BC\right)^2}=\dfrac{AH^2}{BC^2}\)
Ta có \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\Rightarrow AH=\dfrac{24}{5}\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
\(\Rightarrow\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{\left(\dfrac{24}{5}\right)^2}{10^2}=\dfrac{144}{625}\Rightarrow\dfrac{S_{BMNC}}{S_{ABC}}=1-\dfrac{144}{625}=\dfrac{481}{625}\)
d) Ta có: \(\angle ANH+\angle AMH=90+90=180\Rightarrow AMHN\) nội tiếp
\(\Rightarrow\angle ANM=\angle AHM=\angle ABC\left(=90-\angle BHM\right)\)
\(\Rightarrow BMNC\) nội tiếp
\(\Rightarrow\) 4 đường trung trực của các đoạn thẳng BM,MN,NC,CB đồng quy
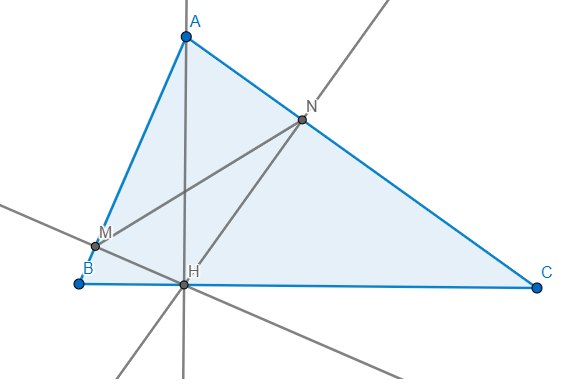
a) Xét ΔAHM vuông tại M và ΔABH vuông tại H có
\(\widehat{HAM}\) chung
Do đó: ΔAHM\(\sim\)ΔABH(g-g)
Suy ra: \(\dfrac{AH}{AB}=\dfrac{AM}{AH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AH^2=AM\cdot AB\)(Đpcm)


