Cho tam giác ABC nội tiếp (O) đường kính AB (AC < BC). Trên dây CB lấy điểm H (với H khác C và B). AH cắt đường tròn tại điểm thứ hai là D. Kẻ HQ vuông góc với AB (với Q thuộc AB)
a, Chứng minh tứ giác BDHQ nội tiếp
b, Biết CQ cắt (O) tại điểm thứ hai F, chứng minh DF // HQ
c, Chứng minh H cách đều các đường thẳng CD, CQ và DQ
d, Gọi M, N lần lượt là hình chiếu của F trên AC và CB. Chứng minh MN, AB, DF đồng quy
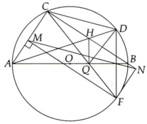
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy

