Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho tam giác ABC. Chứng minh bất đẳng thức sau:
a) AB + BC > AC.
b) AC + BC > AB.
cho tam giác ABC có , góc A = 50o , B : C = 2 : 3 . Bất đẳng thức nào sau đây đúng
A. AC < AB < BC
B. BC < AC < AB
C. AC < BC < AB
D, BC < AB < AC
Cho tam giác ABC,ta có các bất đẳng thức
AB+BC lớn hơn AC
Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
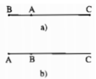
Chứng minh bất đẳng thức của tam giác
AB+BC>AC
AC+BC >AB
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
(dùng bất đẳng thức tam giác)
Một cách chứng minh khác của bất đẳng thức:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường thẳng vuông góc AH đến đường thẳng BC.
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB+ AC> BC.
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.Mình giải cách sau có đúng ko?--Ta có: MB+MAAB (Bất đẳng thức tam giác) MC+MBBC (Bất đẳng thức tam giác) MA+MCAC (Bất đẳng thức tam giác) MB+MA+MC+MB+MA+MCAB+BC+AC 2MA+2MB+2MC 2P MA+MB+MC P (được phần CM)--Ta có: MA+ABMB (Bất đẳng thức tam giác) MB+BCMC (Bất đẳng thức tam giác) MC+ACMA (Bất đẳng...
Đọc tiếp
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
Cho tam giác ABC vuông tại đường cao CH. Trên các cạnh AB và AC lấy tương ứng hai điểm M và N sao cho BM = BC, CN = CH. Chứng minh: al MN vuông góc CA b/ AC + BC < AB + CH Chuẩn bị bài "Quan hệ giữa ba cạnh của tam giác. Bất đẳng thức tam giác"

