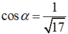Giả sử tiếp tuyến có vtpt là (a;b)
\(\Rightarrow cos45^0=\dfrac{\left|2a-b\right|}{\sqrt{a^2+b^2}.\sqrt{2^2+\left(-1\right)^2}}\Leftrightarrow\sqrt{2}\left|2a-b\right|=\sqrt{5\left(a^2+b^2\right)}\)
\(\Leftrightarrow2\left(2a-b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow3a^2-8ab-3b^2=0\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Rightarrow\) Chọn \(b=-1\Rightarrow\left[{}\begin{matrix}a=-3\\a=\dfrac{1}{3}\end{matrix}\right.\)
\(y'=3x^2-3\Rightarrow\left[{}\begin{matrix}3x^2-3=-3\\3x^2-3=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\sqrt{10}}{3}\\x=-\dfrac{\sqrt{10}}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=0\\y=\dfrac{189-17\sqrt{10}}{27}\\y=\dfrac{189+17\sqrt{10}}{27}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-3x+7\\y=\dfrac{1}{3}\left(x-\dfrac{\sqrt{10}}{3}\right)+\dfrac{189-17\sqrt{10}}{27}\\y=\dfrac{1}{3}\left(x+\dfrac{\sqrt{10}}{3}\right)+\dfrac{189+17\sqrt{10}}{27}\end{matrix}\right.\)