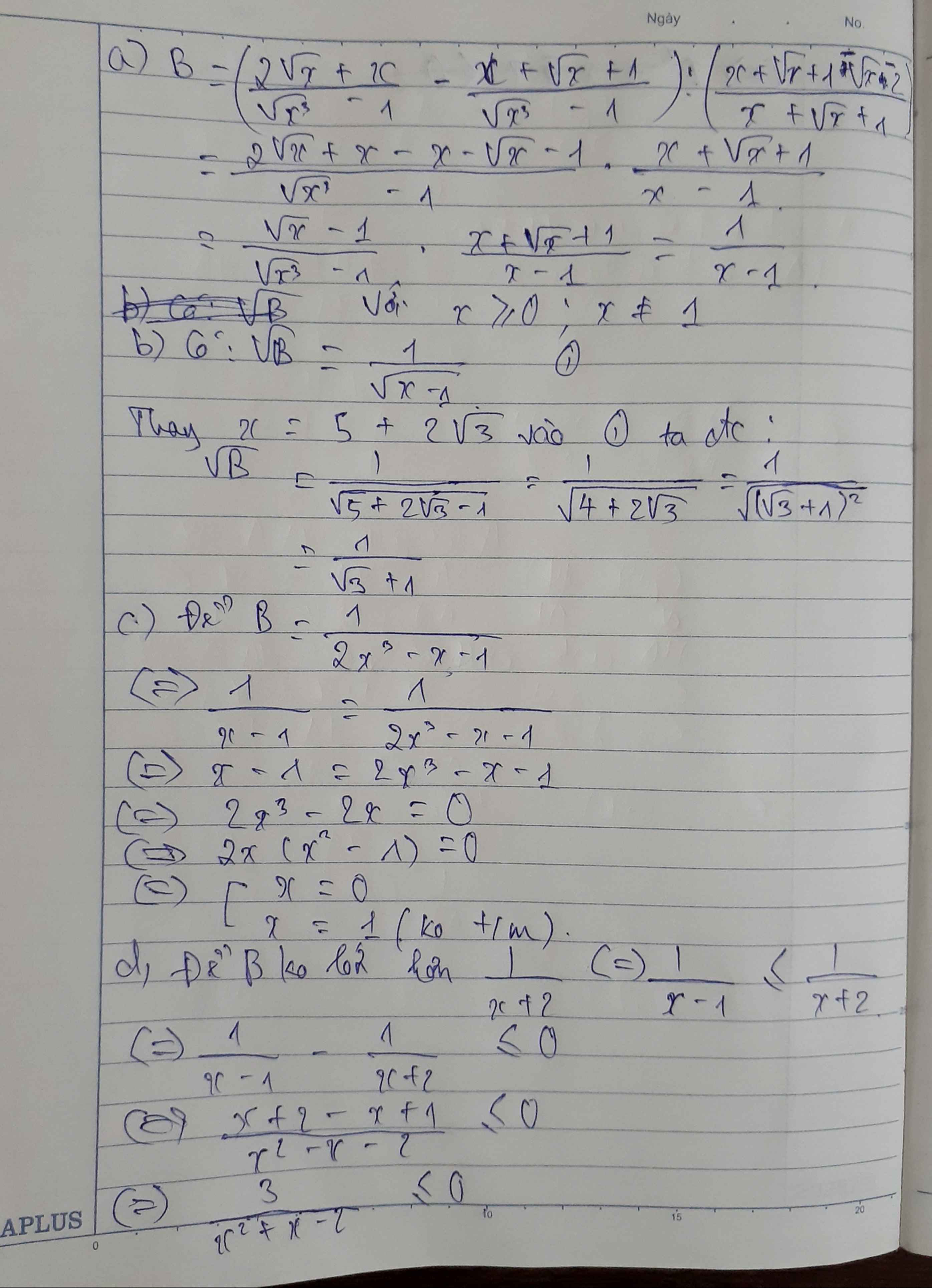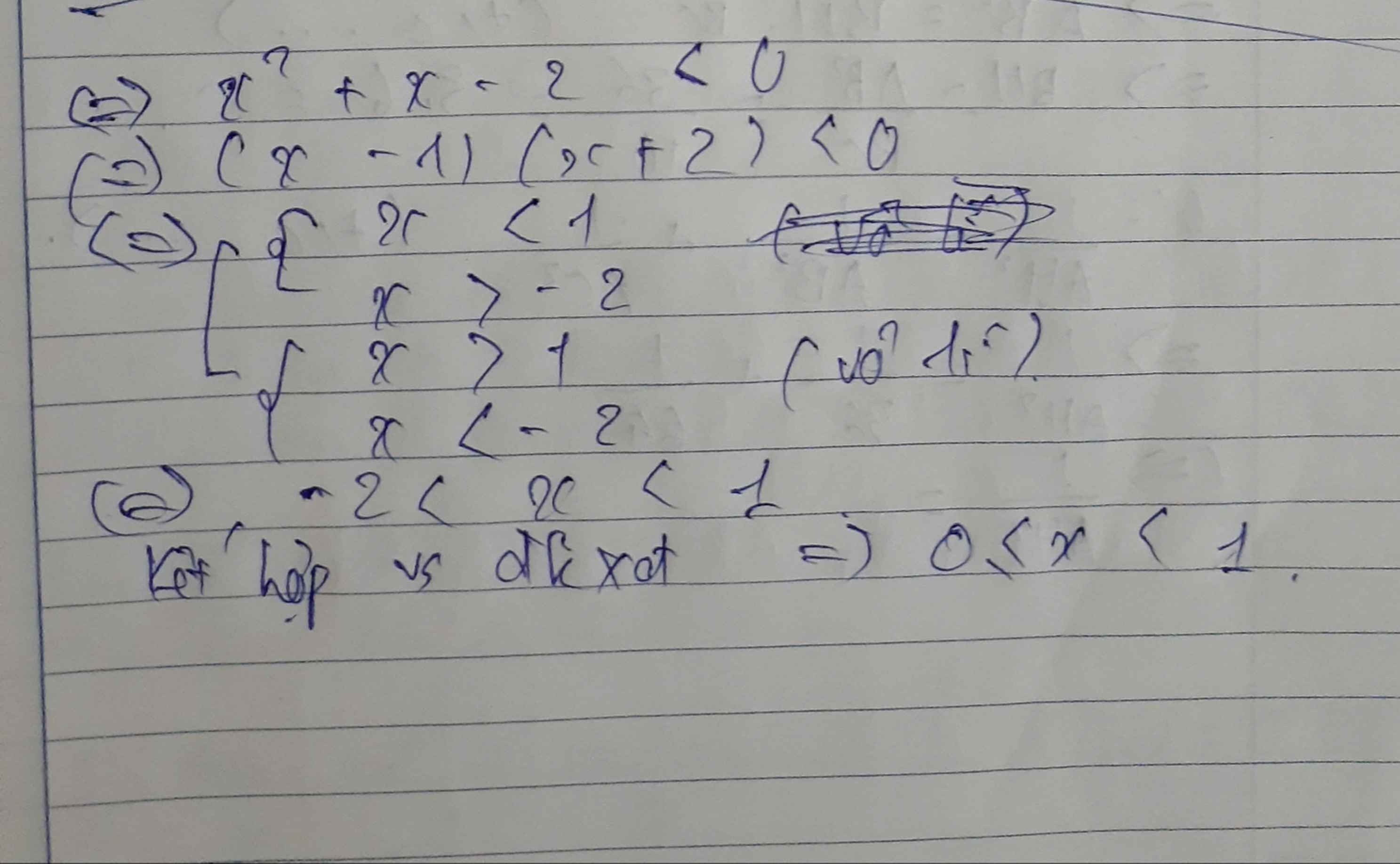cho B=\(\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right)\div\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
a. rút gọn B
b. tính \(\sqrt{B}\) khi \(x=5+2\sqrt{3}\)
c. tìm x để B= \(\dfrac{1}{2x^3-x-1}\)
d. tìm giá trị của x để giá trị của B không lớn hơn giá trị biểu thức \(\dfrac{1}{x+2}\)
Lm nhanh giúp mk nhé mk đang cần gấp
a) \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{x-1}=\dfrac{1}{x-1}\)
a) Ta có: \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x+\sqrt{x}+1}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{1}{x-1}\)