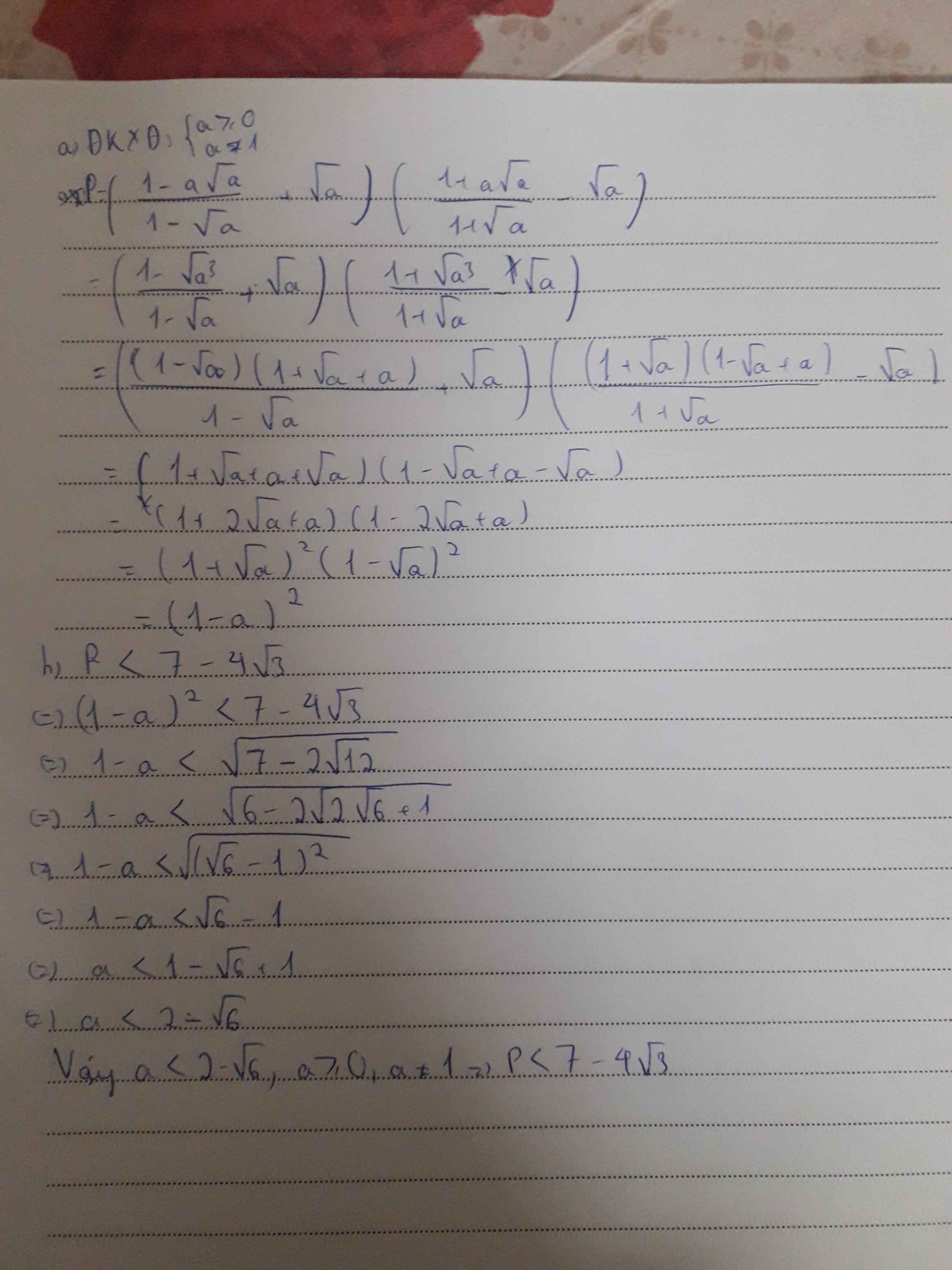a) ĐKXĐ: \(a\ge0;a\ne1\)
\(P=\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left[\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right]\left[\dfrac{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}+a\right)}{1+\sqrt{a}}\right]\)
\(=\left(1+2\sqrt{a}+a\right)\left(1-2\sqrt{a}+a\right)\)
\(=\left(1-a\right)^2\)
b) Để \(P< 7-4\sqrt{3}\)
\(\Rightarrow\left(1-a\right)^2< 7-4\sqrt{3}\)
\(\Leftrightarrow\left|1-a\right|< \left(2-\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{3}-2< a-1< 2-\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}-1< a< 3-\sqrt{3}\)
Vậy \(\sqrt{3}-1< a< 3-\sqrt{3}\) thì \(P< 7-4\sqrt{3}\)