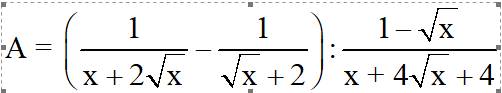\(=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x\left(\sqrt{x}-1\right)+\sqrt{x}-1}\right):\left(\dfrac{x-\sqrt{x}+1}{x+1}\right)\)
\(=\left(\dfrac{x+1}{\left(\sqrt{x}-1\right)\left(x+1\right)}-\dfrac{2}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right).\left(\dfrac{x+1}{x-\sqrt{x}+1}\right)\)
\(=\left(\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+1\right)}\right).\left(\dfrac{x+1}{x-\sqrt{x}+1}\right)=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+1}\)
Lời giải:
Gọi biểu thức là $A$
\(A=\left[\frac{1}{\sqrt{x}-1}-\frac{2}{x(\sqrt{x}-1)+(\sqrt{x}-1)}\right]:\frac{x-\sqrt{x}+1}{x+1}\)
\(=\left[\frac{x+1}{(x+1)(\sqrt{x}-1)}-\frac{2}{(x+1)(\sqrt{x}-1)}\right].\frac{x+1}{x-\sqrt{x}+1}=\frac{x-1}{(x+1)(\sqrt{x}-1)}.\frac{x+1}{x-\sqrt{x}+1}\)
\(=\frac{x-1}{(\sqrt{x}-1)(x-\sqrt{x}+1)}=\frac{\sqrt{x}+1}{x-\sqrt{x}+1}\)