Question

Cho ABCD là hình thang vuông tại A và D đường chéo BD vuông góc với BC .Biết AD=12cm,DC=25cm.Tính độ dài AB,BC và BD

Answer 1

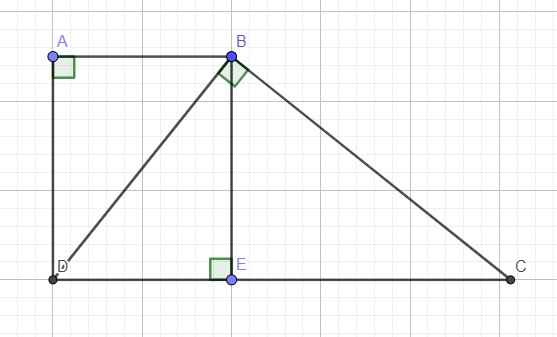
Kẻ BE vuông góc CD \(\Rightarrow ABED\) là hcn (tứ giác 4 góc vuông) \(\Rightarrow AB=DE\)

Đặt \(AB=x>0\) 

Áp dụng định lý Pitago cho tam giác vuông ABD:

\(AB^2+AD^2=BD^2\Leftrightarrow BD^2=x^2+144\) (1)

Áp dụng hệ thức lượng cho tam giác vuông BDC:

\(BD^2=DE.DC\Leftrightarrow BD^2=25x\) (2)

(1);(2) \(\Rightarrow x^2+144=25x\Rightarrow x^2-25x+144=0\Rightarrow\left[{}\begin{matrix}x=16\\x=9\end{matrix}\right.\)

- Với \(AB=16\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=20\left(cm\right)\)

\(BC=\sqrt{DC^2-BD^2}=15\left(cm\right)\)

- Với \(AB=9\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=15\left(cm\right)\)

\(BC=\sqrt{DC^2-BD^2}=20\left(cm\right)\)

Answer 2