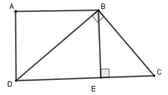
Kẻ BE ⊥ CD tại E
Suy ra tứ giác ABED là hình chữ nhật (vì A ^ = D ^ = E ^ = 90 ∘ ) nên BE = AD = 12cm
Đặt EC = x (0 < x < 25) thì DE = 25 – x
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:
B E 2 = E D . E C ⇔ x ( 25 - x ) = 144 ⇔ x 2 - 25 x + 144 = 0
x 2 - 16 x - 9 x + 144 = 0 <=> x(x – 16) – 9(x – 16) = 0 <=> (x – 16)(x – 9) = 0
⇔ x = 16 x = 9 (thỏa mãn)
Với EC = 16, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 16 2 = 20 (loại)
Với EC = 9, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 9 2 = 15 (nhận)
Vậy BC = 15cm
Đáp án cần chọn là: A

