\(1,x=9\Rightarrow A=\dfrac{2\sqrt{9}+1}{\sqrt{9}}=\dfrac{2.3+1}{3}=\dfrac{7}{3}\)
\(2,B=\dfrac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\dfrac{1}{\sqrt{x}-2}\left(dk:x>0,x\ne4\right)\\ =\dfrac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(3,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-2}{\sqrt{x}}:\dfrac{2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\)
Ta có : \(\left|P\right|+P=0\Leftrightarrow\left|P\right|=-P\)
\(TH_1:x\ge4\\ \dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\Leftrightarrow\dfrac{2\left(\sqrt{x}-2\right)}{2\sqrt{x}+1}=0\Leftrightarrow2\sqrt{x}=4\Leftrightarrow x=4\left(tm\right)\)
\(TH_2:x< 4\\ -\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\left(LD\right)\)
Vậy \(x=4\) thì thỏa mãn đề bài.
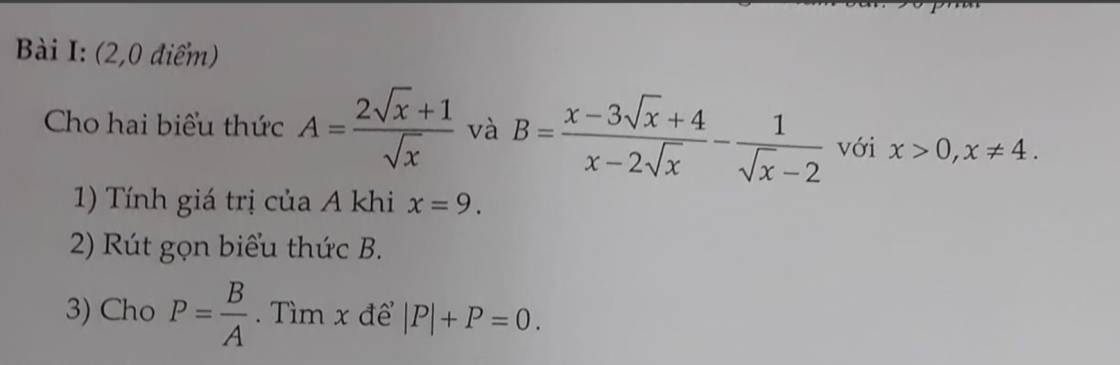



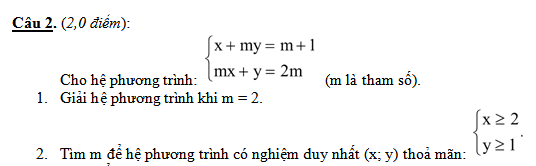





 chỉ cần lm B1 thôi nhé
chỉ cần lm B1 thôi nhé giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
