bài 1: cho tam giác ABC cân tại A. kẻ BD vuông góc với AC và kẻ CE vuông góc với AB. BD và CE cắt nhau tại I
a. chứng minh tam giácBDC=tam giác CEB
b.so sánh góc IBE và góc ICD
c. đường thẳng AI cắt BC tại H. chứng minhAI vuông góc với BC tại H
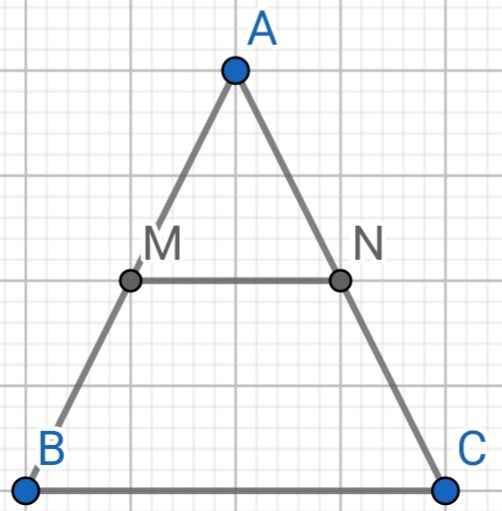
bài 2: cho tam giác ABC. gọi M,N lần lượt là trung điểm của các cạnh AC,AB. trên các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung điểm BD và N là trung điểm EC. chứng minh ba điểm E,A,D thẳng hàng
bài 3: 1. vẽ 1tam giác vuông ABC có góc A =90 độ,AC =4cm, góc C = 60 độ
2.trên tia đối của tia AC lấy điểm D sao cho AD=AC
a. chứng minh tam giácABD=tan giác ABC
b. tam giác BCD có dạng đặc biệt nào? vì sao?
c. tính độ dài các đoạn thẳngBC,AB
bài 4: cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. trên tia AB lấy điểm M sao cho B là trung điểm AM, trêb tia AD lấy điểm N sao cho D là trung điểm AN. chứng minh ba điểm M,C,N thẳng hàng
bài 5: cho tam giác ABCvuông ở A có AB =3cm,AC=4cm
a.tính độ dài cạnh BC
b.trên tia đối của tia AC lấy điểm D sao cho AD=AB. tam giác ABD có dạng đặc biệt nào ? vì sao
c. lấy trên tia đối của tia AB điểm E sao cho AE=AC. chứng minh DE=BC
bài 6: cho góc nhọn xOy. Gọi I là 1 điểm thuộc tia phân giác của góc xOy. kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a. chứng minh IA=IB
b.cho biết OI=10cm, AI=6cm. tính OA
c. gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. so sánh AK và BM?
d. gọi C là giao điểm của OI và MK. chứng minh OC vuông góc với MK
bài 7: cho tam giác ABC cân ở A. trên cạnh AB lấy điểm M, trên tia đối của CA lấy điểm N sai cho BM =CN. gọi K là trung điểm MN. chứng minh ba điểm B,K,C thẳng hàng
bài 8: cho tam giác ABC cân ở A, BAC =108°. Gọi O là 1 điểm nằm trên tia phân giác của góc C sao cho góc CBO=12°. vẽ tam giác đều BOM ( M và A cùng thuộc 1 nửa mặt phẳng bờ BO). chứng minh 3 điểm C,A,M thẳng hàng
mấy bạn giải giùm mình nha. mình cần gấp lắm . thanks mí bạn ngìu nhoak.