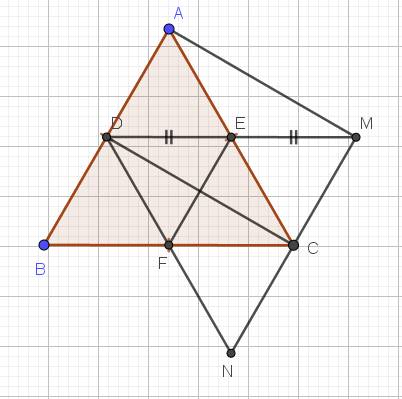
a) Do D là trung điểm AB (gt)
E là trung điểm AC (gt)
\(\Rightarrow\) DE là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE=\dfrac{BC}{2}\) và DE // BC
\(\Rightarrow\)DE // BF (1)
Do E là trung điểm AC (gt)
F là trung điểm BC
\(\Rightarrow\) EF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow EF=\dfrac{AB}{2}\) và EF // AB
\(\Rightarrow\) EF // BD (2)
Từ (1) và (2) \(\Rightarrow\) BDEF là hình bình hành (3)
Ta có: AB = AC = BC (\(\Delta ABC\) đều)
Mà \(DE=\dfrac{BC}{2}\)
\(EF=\dfrac{AB}{2}\)
\(\Rightarrow DE=EF\) (4)
Từ (3) và (4) \(\Rightarrow\) BDEF là hình thoi
b) Do DE = EM (gt)
\(\Rightarrow E\) là trung điểm DM
Tứ giác ADCM có:
E là trung điểm DM (cmt)
E là trung điểm AC (gt)
\(\Rightarrow ADCM\) là hình bình hành (5)
Do \(\Delta ABC\) đều
CE là đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\) CE cũng là đường trung trực của \(\Delta ABC\)
\(\Rightarrow CE\perp AB\)
\(\Rightarrow CE\perp AE\)
\(\Rightarrow\widehat{AEC}=90^0\) (6)
Từ (5) và (6) \(\Rightarrow ADCM\) là hình chữ nhật

