Question

Bài 1. Cho tam giác ABC vuông tại A có AC > AB và đường cao AH. Gọi D, E lần lượt
là hình chiếu của H trên AB, AC.
1) Chứng minh AD. AB = AE. AC và tam giác ADE đồng dạng với tam giác ACB.
2) Cho biết BH = 2cm, CH = 4,5 cm. Tính:
a) Độ dài đoạn thẳng DE.
b) Số đo của góc ABC.
c) Diện tích tam giác ADE.

Answer 1

2)

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)

\(\Leftrightarrow DE^2=2\cdot4.5=9\)

hay DE=3(cm)

b) Xét ΔABH vuông tại H có

\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{3}{2}\)

nên \(\widehat{ABC}\simeq56^0\)

Answer 2

Answer 3

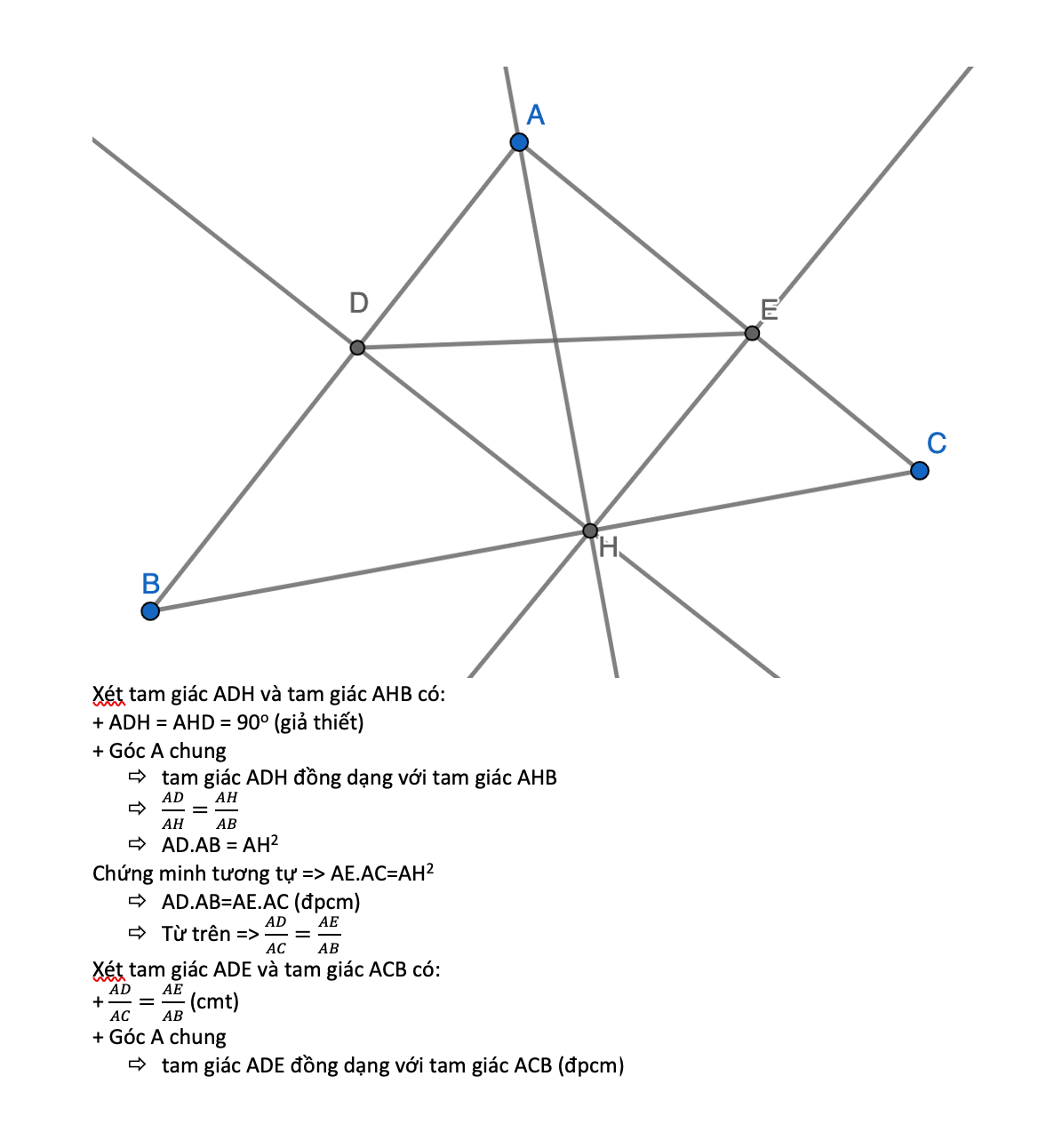
1) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:

\(AD\cdot AB=AH^2\)(1)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:

\(AE\cdot AC=AH^2\)(2)

Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Xét ΔADE vuông tại A và ΔACB vuông tại A có 

\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)(cmt)

Do đó: ΔADE\(\sim\)ΔACB(c-g-c)