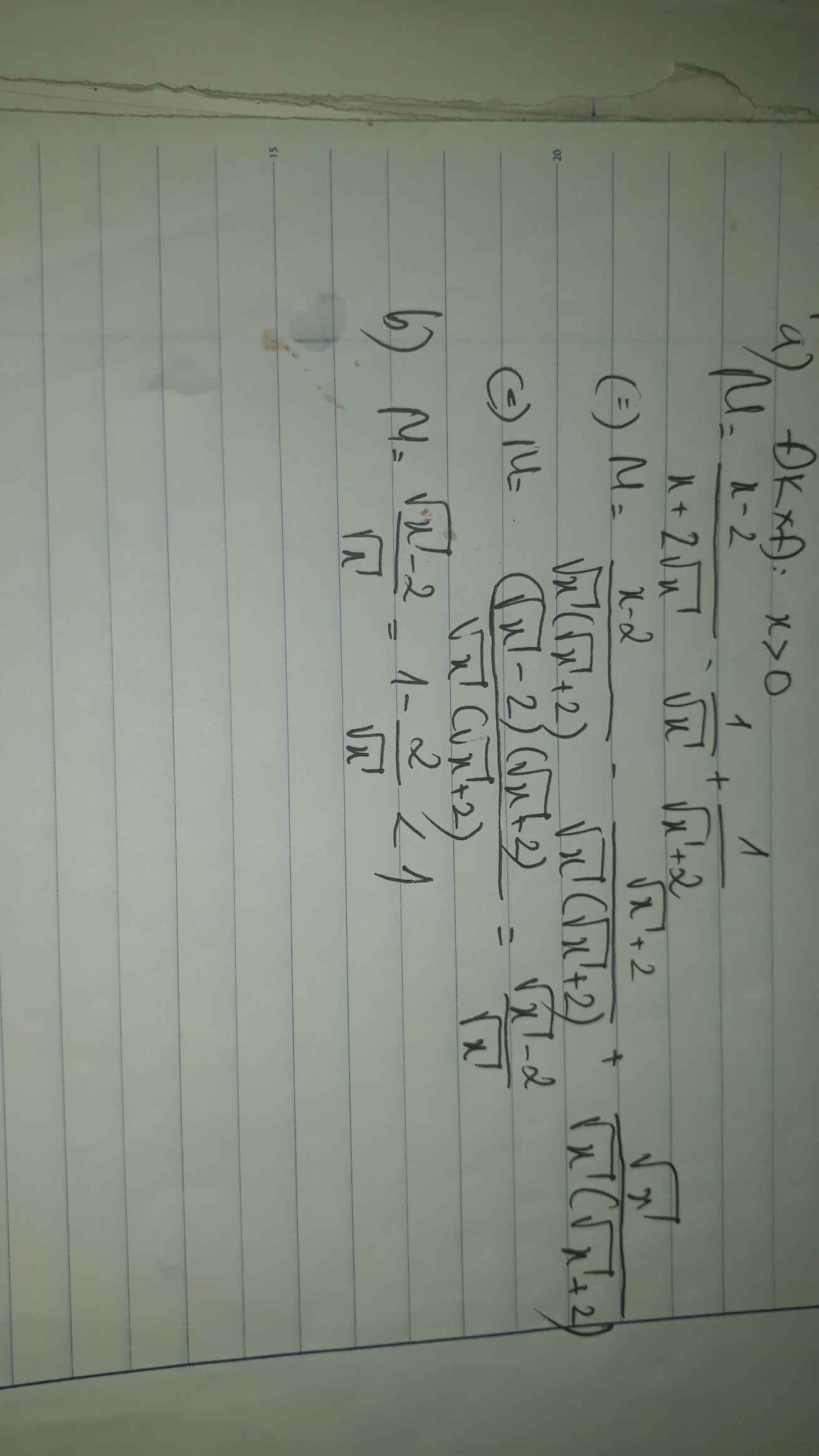a) Ta có: \(M=\dfrac{x-2}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-2-\sqrt{x}-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b) Ta có: M-1
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{-2}{\sqrt{x}}< 0\forall x\) thỏa mãn ĐKXĐ
hay M<1