Các câu hỏi tương tự
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
2
3
x
3
-
m
x
2
-
2
(
3
m
2
-
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 3 x 3 - m x 2 - 2 ( 3 m 2 - 1 ) x + 2 3 có hai điểm cực trị có hoành độ x 1 , x 2 sao cho x 1 x 2 + 2 ( x 1 + x 2 ) = 1
A. m = 0
B. m = - 2 3
C. m = 2 3
D. m = - 1 2
Với giá trị nào của m, hàm số
y
x
3
+
2
(
m
-
1
)
x
2
+
(
m
2
-
4
m
+
1
)
x
+
2
(
m
2
+
1
)
có hai điểm cực trị
x
1...
Đọc tiếp
Với giá trị nào của m, hàm số y = x 3 + 2 ( m - 1 ) x 2 + ( m 2 - 4 m + 1 ) x + 2 ( m 2 + 1 ) có hai điểm cực trị x 1 , x 2 thỏa mãn 1 x 1 + 1 x 2 = x 1 + x 2 2
A. m = 5 hoặc m = 1
B. m = 2 hoặc m = 1
C. m = 5
D. m = 1
Tìm các giá trị của tham số m để hàm số:
y
1
3
m
x
3
-
(
m
-
1
)
x
2
+
3
(
m
-
2
)
x
+...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số: y = 1 3 m x 3 - ( m - 1 ) x 2 + 3 ( m - 2 ) x + 1 6 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1
A. 1 - 6 2 < m < 1 + 6 2 .
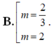
C. m ∈ 1 - 6 2 ; 1 + 6 2 \ 0 .
D. m = 2 .
Biết
a
b
(trong đó
a
b
là phân số tối giản,
a
,
b
∈
N
*
) là giá trị thực của tham số m để hàm số
y
2
x
3
-
3
m
x
2
-
6
(
3
m
2...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản, a , b ∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 m x 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P=a+2b.
![]()
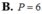
![]()
![]()
Tìm tất các giá trị thực của tham số m để hàm số
y
1
3
x
3
+
(
m
+
3
)
x
2
+
4
(
m
+
3
)
x
+
m
3...
Đọc tiếp
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn -2< x 1 < x 2
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
Cho hàm số bậc 4 y f(x) có đồ thị như hình vẽ bên. Biết hàm số y f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 x1+2, f(x1) + f(x3) +dfrac{2}{3}f(x2) 0 và (C) nhận đường thẳng x x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số dfrac{S_1+S_2}{S_3+S_4} gần với kết quả nào nhất :
Đọc tiếp
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Tìm tất các giá trị thực của tham số m để hàm số
y
1
3
x
3
+
(
m
+
3
)
x
2
+
4
(
m
+...
Đọc tiếp
Tìm tất các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m + 3 ) x 2 + 4 ( m + 3 ) x + m 3 - m đạt cực trị tại x 1 , x 2 thỏa mãn - 1 < x 1 < x 2
A. - 7 2 < m < - 2 .
B. - 3 < m < 1 .
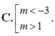
D. - 7 2 < m < - 3 .
Gọi S là tập các giá trị dương của tham số m sao cho hàm số
y
x
3
-
3
m
x
2
+
9
x
-
m
đạt cực trị tại
x
1
,
x
2
thỏa mãn
x
1
-
x...
Đọc tiếp
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = x 3 - 3 m x 2 + 9 x - m đạt cực trị tại x 1 , x 2 thỏa mãn x 1 - x 2 ≤ 2 . Biết S=(a;b]. Tính T=b-a
![]()
![]()
![]()
![]()
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y
x
3
-
3
m
x
2
+
27
x
+
3
m
-
2
đạt cực trị tại
x
1
,
x
2
thỏa mãn
x
1
,
x
2...
Đọc tiếp
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = x 3 - 3 m x 2 + 27 x + 3 m - 2 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 , x 2 ≤ 5 . Biết S = (a;b]. Tính T = 2b - a.
A. T = 51 + 6
B. T = 61 + 3
C. T = 61 - 3
D. T = 51 - 6
