Question

1) Cho tam giác ABC cân tại A có AD là đường phân giác

a) C/m: tam giác ABD= tam giác ACD

b) C/m: AD là đường trung trực của BC

c) Từ D kẻ DM vuông góc với AB, DN vuông góc với AC.

C/m: tam giác AMN cân 

kẻ hình giúp e vs ak

Answer 1

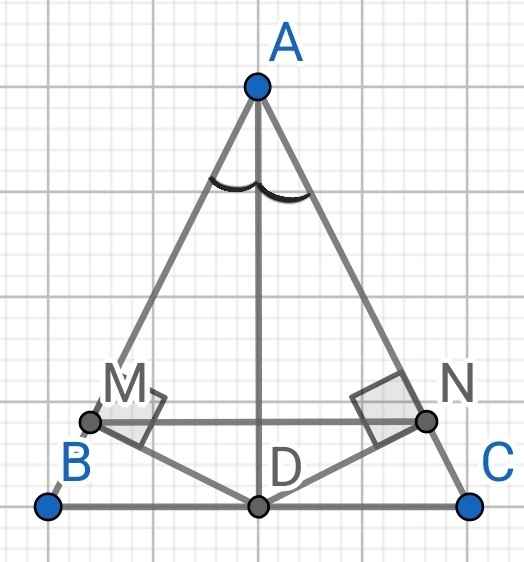
`a)`Xét có :

`AB = AC (ΔABC` cân)

\(\widehat{BAD}=\widehat{CAD}\)`( AD` là phân giac)

`AB = AC`(`ΔABC` cân)

`=>  ΔABD =ΔACD (c-g-c)`

`b) `ΔABC` cân tại `A`

Có : `AD` là đường phân giác \(\widehat{A}\) ứng với cạnh `BC`

`=> AD` đồng thời là đường trung trực của `ΔABC`

`c)`Xét `ΔMBD` và `ΔNCD`có :

\(\widehat{BMD}-\widehat{DNC}=90^0\)

`BD = DC`(AD là trung trực)

\(\widehat{B}=\widehat{C}\)(`ΔABC` cân)

`=>  ΔMBD =ΔNCD(ch-gn)`

`=> BM = NC`

Mà `AB = AC`

`=> AM = AN`

`=> ΔAMN` cân

Answer 2

a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Do AD là đường phân giác của ∆ABC (gt)

⇒ ∠BAD = ∠CAD

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

b) ∆ABC cân tại A (gt)

AD là đường phân giác của ∆ABC (gt)

⇒ AD cũng là đường trung trực của ∆ABC

⇒ AD là đường trung trực của BC

c) Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét hai tam giác vuông: ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

⇒ ∆ADM = ∆ADN (cạnh huyền - góc nhọn)

⇒ AM = AN (hai cạnh tương ứng)

⇒ ∆AMN cân tại A