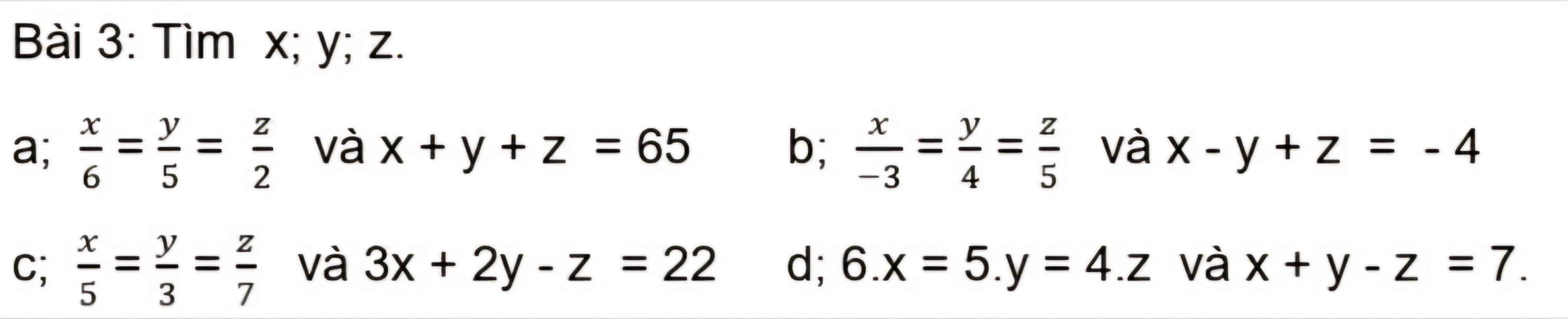\(a;\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{z}{2}\) và `x+y+z = 65`
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y+z}{6+5+2}=\dfrac{65}{13}=5\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{6}=5\\\dfrac{y}{5}=5\\\dfrac{z}{2}=5\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=5.6\\y=5.5\\z=5.2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=30\\y=25\\z=10\end{matrix}\right.\)
Vậy `(x;y;z)=(30;25;10)`
`b;`\(\dfrac{x}{-3}=\dfrac{y}{4}=\dfrac{z}{5}\) và \(x-y+z=-4\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\Rightarrow\dfrac{x}{-3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x-y+z}{-3-4+5}=\dfrac{-4}{-2}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{-3}=2\\\dfrac{y}{4}=2\\\dfrac{z}{5}=2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=2.-3\\y=2.4\\z=2.5\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=-6\\y=8\\z=10\end{matrix}\right.\)
Vậy `(x;y;z) = (-6;8;10)`
`#1194`
`c,`
Ta có: `x/5 = y/3 = z/7`
`(3x)/15 = (2y)/6 = z/7`
AD tính chất dãy tỉ số = nhau ta có:
`(3x)/15 = (2y)/6 = z/7 = (3x + 2y - z)/(15 + 6 - 7) = 22/14 = 11/7`
Suy ra: `x/5 = y/3 = z/7 = 11/7`
`x = (5*11)/7 = 55/7`
`y = (3*11)/7 = 33/7`
`z = (7*11)/7 = 11`
Vậy, `x = 55/7; y = 33/7; z = 11`
`d,`
Ta có: `6x = 5y = 4z`
\(\dfrac{x}{\dfrac{1}{6}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{z}{\dfrac{1}{4}}\)
AD tính chất dãy tỉ số = nhau ta có:
\(\dfrac{x}{\dfrac{1}{6}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y-z}{\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{4}}=\dfrac{7}{\dfrac{7}{60}}=60\)
Suy ra: \(\dfrac{x}{\dfrac{1}{6}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{z}{\dfrac{1}{4}}=60\)
`x=60*1/6 = 10; y = 60*1/5=12; z=60*1/4=15`
Vậy, `x = 10; y = 12; z = 15.`