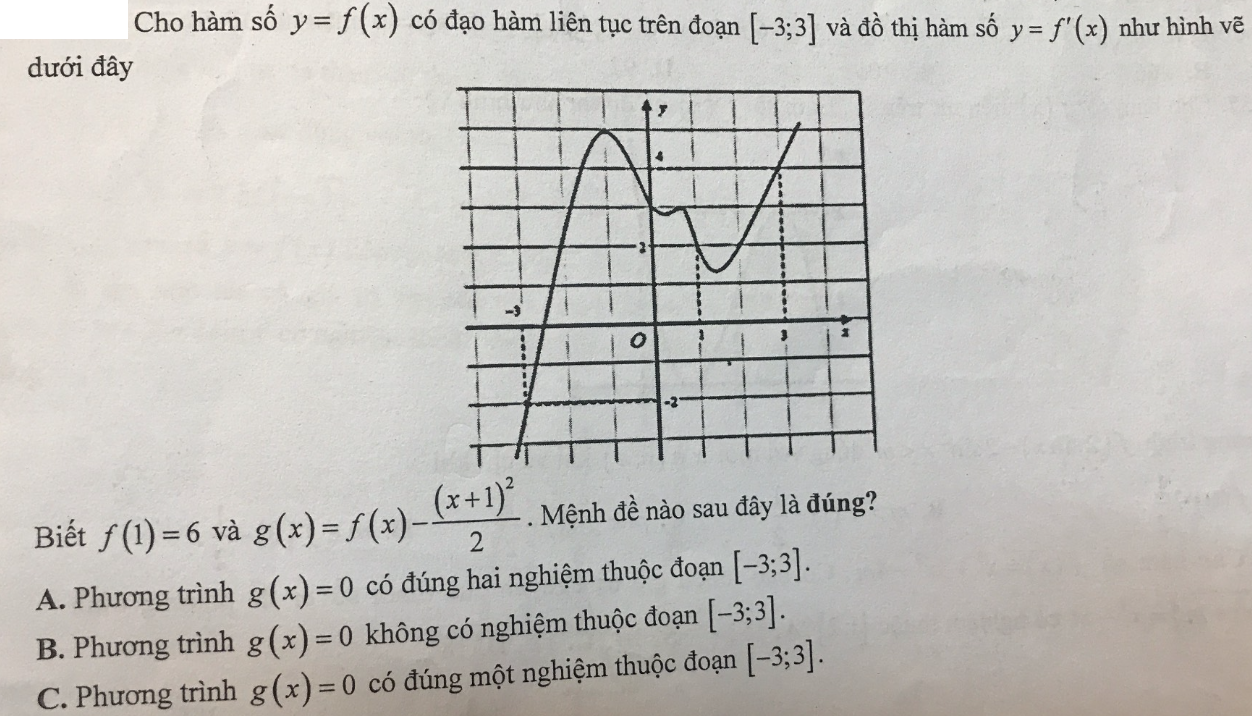\(g'\left(x\right)=f'\left(x\right)-\left(x+1\right)=0\Rightarrow f'\left(x\right)=x+1\)
Vẽ \(y=x+1\) lên cùng hệ trục thấy pt có 3 nghiệm \(x=-3;1;3\)
\(g\left(1\right)=f\left(1\right)-2=4\)
\(g\left(-3\right)=f\left(-3\right)-2\)
\(g\left(3\right)=f\left(3\right)-8\)
Đến đây vấn đề là cần xác định dấu của \(g\left(-3\right)\) và \(g\left(3\right)\)
Từ đồ thị thấy diện tích phần giới hạn bởi \(f'\left(x\right)\) và trục Ox từ đoạn \(x=1\) đến \(x=3\) lớn hơn 3 đơn vị (có ít nhất là 3 ô vuông)
\(\Rightarrow\int\limits^3_1f'\left(x\right)dx>3\Rightarrow f\left(3\right)-f\left(1\right)>3\Rightarrow f\left(3\right)>9\)
\(\Rightarrow g\left(3\right)>1>0\)
Phần diện tích giới hạn bởi \(f'\left(x\right)\) và Ox từ \(x=-3\) đến \(x=1\) lớn hơn 6 đơn vị (lớn hơn khá nhiều, đếm được 7 ô vuông trọn vẹn - chú ý là phần nằm dưới trục Ox cần trừ đi, nhưng đoạn này khá nhỏ)
\(\Rightarrow f\left(1\right)-f\left(-3\right)>6\Rightarrow f\left(-3\right)< 0\) \(\Rightarrow g\left(-3\right)=f\left(-3\right)-2< 0\)
Do đó \(g\left(x\right)=0\) có đúng 1 nghiệm