a. Sai, hàm có 3 cực trị
b. Sai
\(u=x^2+1\Rightarrow u'=2x=0\Rightarrow x=0\)
\(u\left(0\right)=1\)
\(y=3\) cắt u(x) tại hoành độ a và b; y=4 cắt u(x) tại c và d
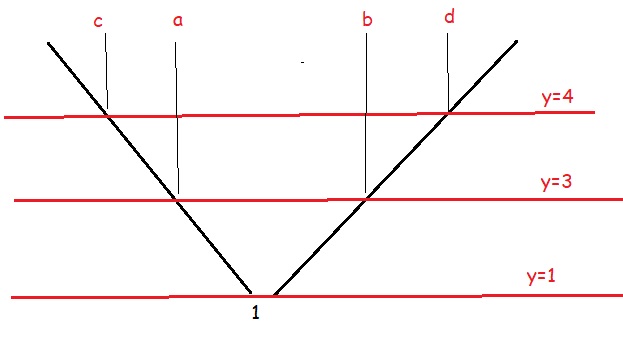
Dẫn tới BBT hàm \(f\left(u\right)\) như sau:
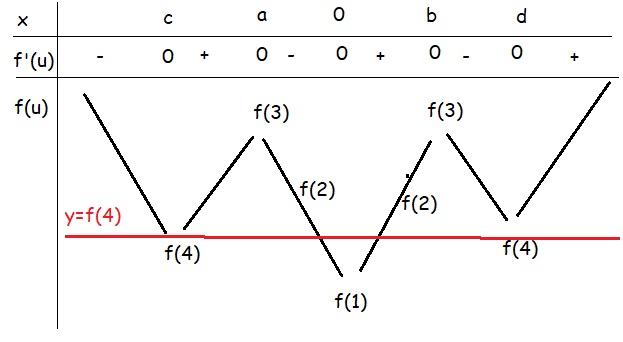
Hàm có 5 cực trị.
c. Đúng
Từ BBT suy ra \(y=f\left(3\right)\) cắt \(f\left(u\right)\) tại 4 điểm (2 nghiệm đơn và 2 nghiệm kép)
d.Sai
\(f\left(1\right)+f\left(3\right)=f\left(2\right)+f\left(4\right)\)
\(\Rightarrow f\left(4\right)-f\left(1\right)=f\left(3\right)-f\left(2\right)>0\)
Do đó \(f\left(1\right)\) nằm thấp hơn \(f\left(4\right)\) giống hình trên
Suy ra \(f\left(u\right)=f\left(4\right)\) có 4 nghiệm (2 đơn 2 kép)






