Chờ xíu hồi nãy bận coi đá banh :D
5.
\(f\left(x\right)=-x+4-\dfrac{9}{x+2}\) nên \(y=-x+4\Leftrightarrow x+y-4=0\) là TCX và \(x=-2\) là TCĐ
Gọi \(M\left(x;\dfrac{-x^2+2x-1}{x+2}\right)\) là điểm thuộc (C)
K/c từ M đến TCĐ là \(\left|x-\left(-2\right)\right|=\left|x+2\right|\)
K/c đến TCX là \(\dfrac{\left|x+\dfrac{-x^2+2x-1}{x+2}-4\right|}{\sqrt{1^2+1^2}}=\dfrac{9}{\sqrt{2}\left|x+2\right|}\)
Do đó tổng khoảng cách là:
\(S=\left|x+2\right|+\dfrac{9}{\sqrt{2}\left|x+2\right|}\ge2\sqrt{\left|x+2\right|.\dfrac{9}{\sqrt{2}\left|x+2\right|}}=\dfrac{6}{\sqrt[4]{2}}\)
6.
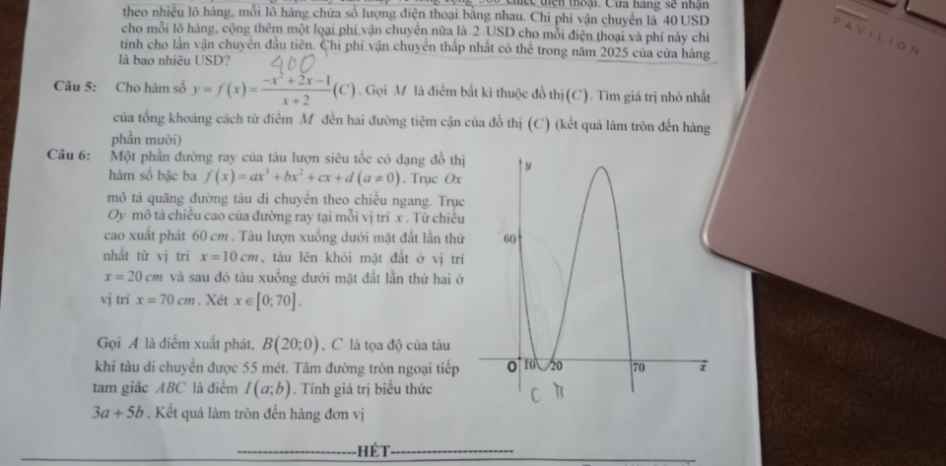
Pt \(f\left(x\right)=0\) có 3 nghiệm \(x=10;20;70\) nên f(x) có dạng:
\(f\left(x\right)=a\left(x-10\right).\left(x-20\right)\left(x-70\right)\)
\(f\left(0\right)=60\Rightarrow a.\left(-10\right).\left(-20\right).\left(-70\right)=60\)
\(\Rightarrow a=-\dfrac{3}{700}\Rightarrow f\left(x\right)=-\dfrac{3}{700}.\left(x-10\right)\left(x-20\right)\left(x-70\right)\)
\(x_C=55\Rightarrow y_C=y\left(55\right)=\dfrac{405}{4}\) \(\Rightarrow C\left(55;\dfrac{405}{4}\right)\)
Cần tìm tọa độ tâm đường tròn ngoại tiếp ABC với \(A\left(0;60\right);B\left(20;0\right)\) và \(C\left(55;\dfrac{405}{4}\right)\)
Có vài cách giải bài toán cơ bản này
Gọi M là trung điểm AB \(\Rightarrow M\left(10;30\right)\), N là trung điểm AC \(\Rightarrow N\left(\dfrac{55}{2};\dfrac{645}{8}\right)\)
\(\overrightarrow{AB}=\left(20;-60\right)=20\left(1;-3\right)\)
\(\overrightarrow{AC}=\left(55;\dfrac{165}{4}\right)=\dfrac{55}{4}\left(4;3\right)\)
Trung trực của AB có pt: \(1\left(x-10\right)-3\left(y-30\right)=0\Leftrightarrow x-3y=-80\)
Trung trực AC có pt: \(4\left(x-\dfrac{55}{2}\right)+3\left(y-\dfrac{645}{8}\right)=0\Leftrightarrow4x+3y=\dfrac{2815}{8}\)
I là nghiệm của hệ: \(\left\{{}\begin{matrix}x-3y=-80\\4x+3y=\dfrac{2815}{8}\end{matrix}\right.\)
\(\Rightarrow I\left(\dfrac{435}{8};\dfrac{1075}{24}\right)\)