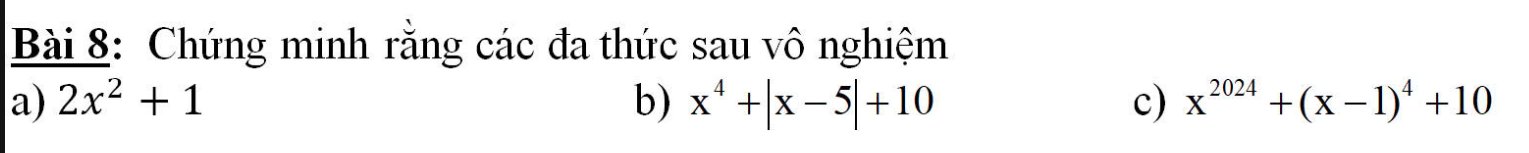a: \(2x^2>=0\forall x\)
=>\(2x^2+1>=1>0\forall x\)
=>Đa thức 2x2+1 không có nghiệm
b: \(x^4>=0\forall x;\left|x-5\right|>=0\forall x\)
Do đó: \(x^4+\left|x-5\right|>=0\forall x\)
=>\(x^4+\left|x-5\right|+10>=10>0\forall x\)
=>Đa thức \(x^4+\left|x-5\right|+10\) không có nghiệm
c: \(x^{2024}>=0\forall x;\left(x-1\right)^4>=0\forall x\)
Do đó: \(x^{2024}+\left(x-1\right)^4>=0\forall x\)
=>\(x^{2024}+\left(x-1\right)^4+10>=10>0\forall x\)
=>Đa thức \(x^{2024}+\left(x-1\right)^4+10\) không có nghiệm
a) Với mọi x thuộc R, ta luôn có:
\(x^2\ge0\Rightarrow2x^2\ge0\Rightarrow2x^2+1\ge1>0\)
Vậy đa thức \(2x^2+1\) vô nghiệm
b) Với mọi x thuộc R, ta luôn có:
\(\left\{{}\begin{matrix}x^4\ge0\\\left|x-5\right|\ge0\end{matrix}\right.\Rightarrow x^4+\left|x-5\right|>0\) (Do không cùng xảy ra dấu "=")
\(\Rightarrow x^4+\left|x-5\right|+10>10>0\)
Vậy đa thức \(x^4+\left|x-5\right|+10\) vô nghiệm
c) Với mọi x thuộc R, ta luôn có:
\(\left\{{}\begin{matrix}x^{2024}\ge0\\\left(x-1\right)^4\ge0\end{matrix}\right.\Rightarrow x^{2024}+\left(x-1\right)^4>0\) (Do không cùng xảy ra dấu "=")
\(\Rightarrow x^{2024}+\left(x-1\right)^4+10>10>0\)
Vậy đa thức \(x^{2024}+\left(x-1\right)^4+10\) vô nghiệm