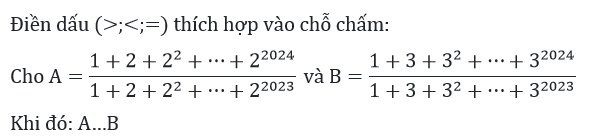\(A=\dfrac{1+2+2^2+...+2^{2023}+2^{2024}}{1+2+2^2+...+2^{2023}}=1+\dfrac{2^{2024}}{1+2+2^2+...+2^{2023}}\)
\(B=\dfrac{1+3+3^2+...+3^{2023}+3^{2024}}{1+3+3^2+...+3^{2023}}=1+\dfrac{3^{2024}}{1+3+3^2+...+3^{2023}}\)
Đặt \(C=1+2+2^2+...+2^{2023}\)
\(2C=2+2^2+2^3+...+2^{2024}\)
\(2C-C=2^{2024}-1\)
\(\Rightarrow C=2^{2024}-1\)
\(\Rightarrow\dfrac{2^{2024}}{1+2+...+2^{2023}}=\dfrac{2^{2024}}{2^{2024}-1}=\dfrac{2^{2024}-1+1}{2^{2024}-1}=1+\dfrac{1}{2^{2024}-1}\)
\(\Rightarrow A=2+\dfrac{1}{2^{2024}-1}\)
Do \(2^{2024}-1>1\Rightarrow\dfrac{1}{2^{2024}-1}< 1\Rightarrow A< 3\) (1)
Đặt \(D=1+3+3^2+...+3^{2023}\)
\(3D=3+3^2+...+3^{2024}\)
\(3D-D=3^{2024}-1\)
\(\Rightarrow D=\dfrac{3^{2024}-1}{2}\)
\(\Rightarrow\dfrac{3^{2024}}{1+3+...+3^{2024}}=\dfrac{3^{2024}}{\dfrac{3^{2024}-1}{2}}=\dfrac{2.3^{2024}}{3^{2024}-1}=\dfrac{2\left(3^{2024}-1\right)+2}{3^{2024}-1}=2+\dfrac{2}{3^{2024}-1}\)
\(\Rightarrow B=3+\dfrac{2}{3^{2024}-1}>3\) (2)
(1);(2) \(\Rightarrow A< B\)