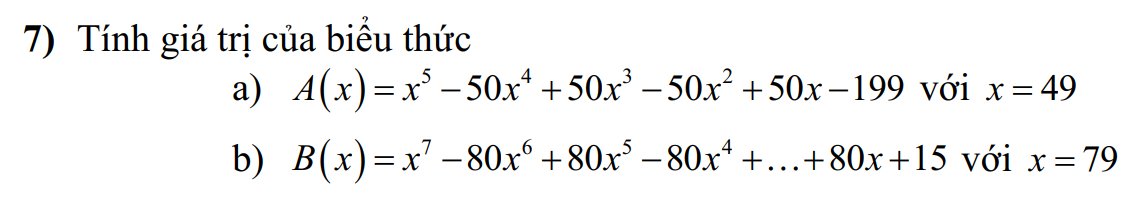a.
\(x=49\Rightarrow50=x+1\)
\(\Rightarrow A\left(x\right)=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x-199\)
\(=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-199\)
\(=x-199=49-199=-150\)
b.
\(x=79\Rightarrow x+1=80\)
\(\Rightarrow B\left(x\right)=x^7-\left(x+1\right)x^6+\left(x+1\right)x^6-\left(x+1\right)x^4+...+\left(x+1\right)x+15\)
\(=x^7-x^7-x^6+x^6+x^5-x^5-x^4+...+x^2+x+15\)
\(=x+15=79+15=94\)
a) \(A\left(x\right)=x^5-50x^4+50x^3-50x^2+50x-199\)
Ta có : \(x=49\Rightarrow x+1=50\)
\(\Rightarrow A\left(x\right)=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x+1\right)x-199\)
\(\Rightarrow A\left(x\right)=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-199\)
\(\Rightarrow A\left(x\right)=x-199=49-199=-150\)