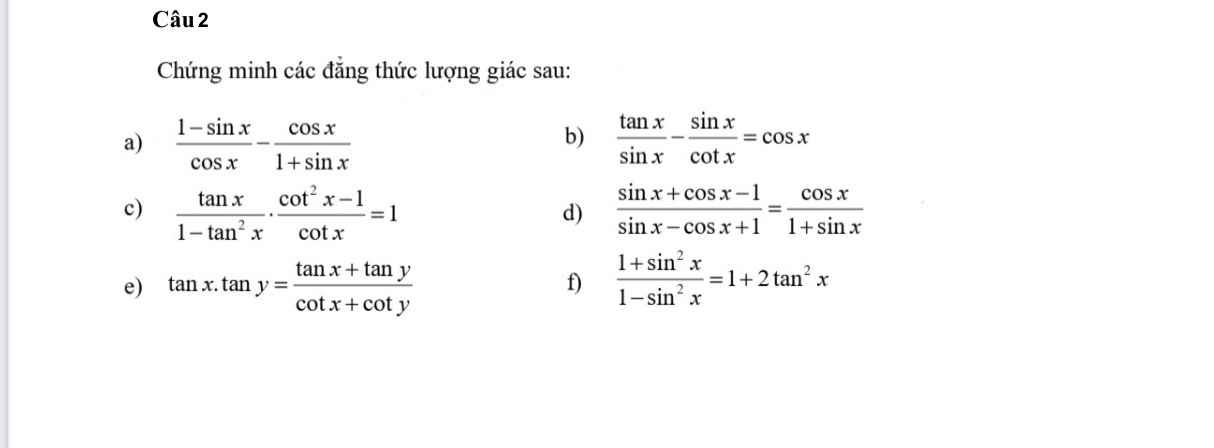e: \(\dfrac{tanx+tany}{cotx+coty}=\dfrac{\dfrac{sinx}{cosx}+\dfrac{siny}{cosy}}{\dfrac{cosx}{sinx}+\dfrac{cosy}{siny}}\)
\(=\dfrac{sinx\cdot cosy+cosx\cdot siny}{cosx\cdot cosy}:\dfrac{siny\cdot cosx+sinx\cdot cosy}{sinx\cdot siny}\)
\(=\dfrac{sinx}{cosx}\cdot\dfrac{siny}{cosy}=tanx\cdot tany\)
b: \(\dfrac{tanx}{sinx}-\dfrac{sinx}{cotx}=\dfrac{sinx}{cosx\cdot sinx}-sinx:\dfrac{cosx}{sinx}\)
\(=\dfrac{1}{cosx}-\dfrac{sin^2x}{cosx}=\dfrac{1-sin^2x}{cosx}=\dfrac{cos^2x}{cosx}=cosx\)
c: \(\dfrac{tanx}{1-tan^2x}\cdot\dfrac{cot^2x-1}{cotx}\)
\(=\dfrac{tanx}{1-\left(\dfrac{sinx}{cosx}\right)^2}\cdot\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-1}{cotx}\)
\(=\dfrac{tanx}{cotx}\cdot\dfrac{\dfrac{cos^2x}{sin^2x}-1}{1-\dfrac{sin^2x}{cos^2x}}=\dfrac{tanx}{cotx}\cdot\dfrac{\dfrac{cos^2x-sin^2x}{sin^2x}}{\dfrac{cos^2x-sin^2x}{cos^2x}}\)
\(=\dfrac{tanx}{cotx}\cdot\left(\dfrac{cos^2x-sin^2x}{sin^2x}\cdot\dfrac{cos^2x}{cos^2x-sin^2x}\right)\)
\(=\dfrac{tanx}{cotx}\cdot\dfrac{cos^2x}{sin^2x}=\left(\dfrac{sinx}{cosx}:\dfrac{cosx}{sinx}\right)\cdot\dfrac{cos^2x}{sin^2x}\)
\(=\dfrac{sin^2x}{cos^2x}\cdot\dfrac{cos^2x}{sin^2x}=1\)