5)
a) BE là trung tuyến của ΔABC ⇒ E là trung điểm của AC
CF là trung tuyến của ΔABC ⇒ F là trung điêm của AB
⇒ EF là đường trung bình của ΔABC
⇒ \(EF=\dfrac{1}{2}BC\) (1)
I là trung điểm của BG
K là trung điêm của CG
⇒ IK là đường trung bình của ΔBGC
\(\Rightarrow IK=\dfrac{1}{2}BC\) (2)
Từ (1) và (2) \(\Rightarrow EF=IK\left(=\dfrac{1}{2}BC\right)\)
b) EF là đường trung bình của ΔABC
⇒ EF//BC (3)
IK là đường trung bình của ΔBGC
⇒ IK//BC (4)
Từ (3) và (4) ⇒ EF//IK
Bài 5
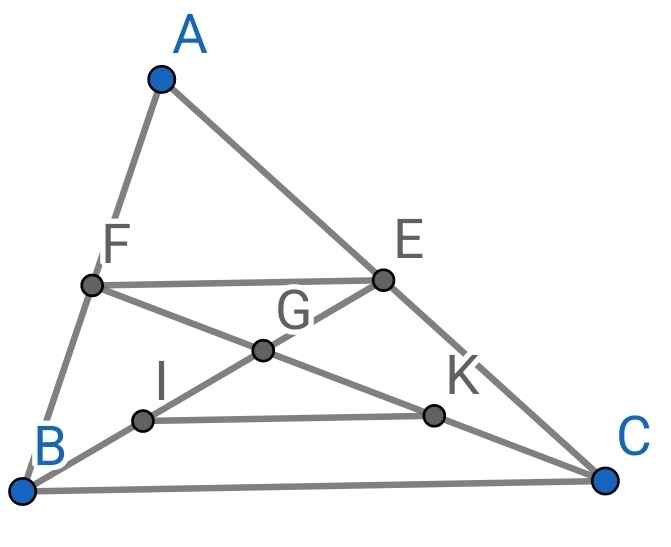a) ∆ABC có:
E là trung điểm của AC (do BE là đường trung tuyến)
F là trung điểm của AC (do CF là đường trung tuyến)
⇒ EF là đường trung bình của ∆ABC
⇒ EF // BC và EF = BC : 2
∆GBC có:
I là trung điểm của BG (gt)
K là trung điểm của CG (gt)
⇒ IK là đường trung bình của ∆GBC
⇒ IK // BC và IK = BC : 2
Mà EF = BC : 2 (cmt)
⇒ EF = IK
b) Do EF // BC (cmt)
IK // BC (cmt)
⇒ EF // IK
