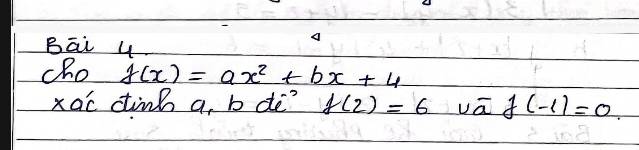\(\left\{{}\begin{matrix}f\left(2\right)=6\\f\left(-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\cdot2^2+b\cdot2+4=6\\a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+4=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4a+2b=2\\a-b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b=1\\a-b=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=-3\\a-b=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-1\\b=a+4=-1+4=3\end{matrix}\right.\)
f(2) = 6
⇒ a.2² + b.2 + 4 = 6
⇔ 4a + 2b = 6 - 4
⇔4a + 2b = 2
⇔ 2a + b = 1
⇔ b = 1 - 2a (1)
f(-1) = 0
⇒ a.(-1)² + b.(-1) + 4 = 0
⇔ a - b + 4 = 0 (2)
Thế (1) vào (2), ta có:
a - (1 - 2a) + 4 = 0
⇔ a - 1 + 2a + 4 = 0
⇔ 3a + 3 = 0
⇔ 3a = -3
⇔ a = -3 : 3
⇔ a = -1
Thế a = -1 vào (1), ta có:
b = 1 - 2.(-1) = 3
Vậy a = -1; b = 3