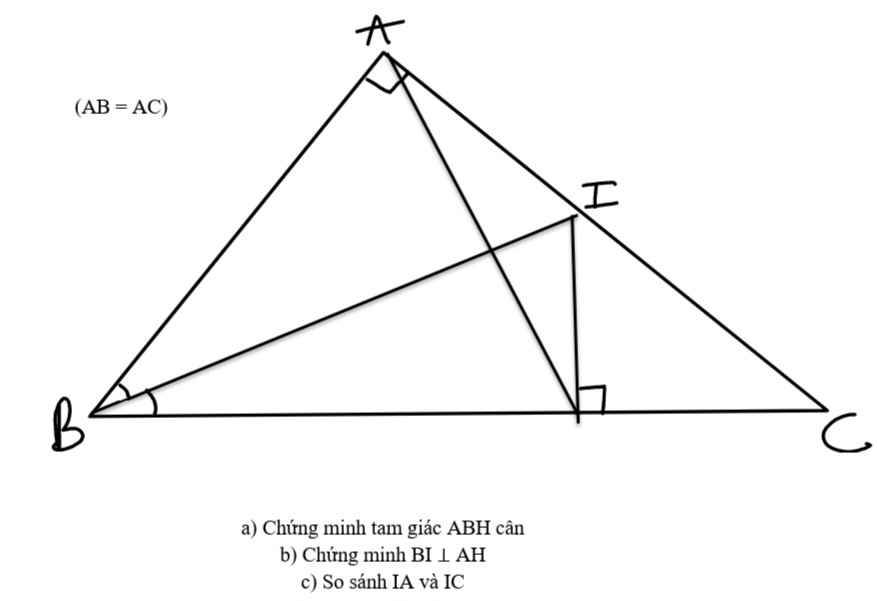
a) Xét hai tam giác vuông: ∆ABI và ∆HBI có:
BI là cạnh chung
∠ABI = ∠HBI (gt)
⇒ ∆ABI = ∆HBI (cạnh huyền - góc nhọn)
⇒ AB = HB (hai cạnh tương ứng)
⇒ ∆ABH cân tại B
b) Do ∆ABI = ∆HBI (cmt)
⇒ AI = HI
⇒ I nằm trên đường trung trực của AH (1)
Do AB = BH (cmt)
⇒ B nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BI là đường trung trực của AH
⇒ BI ⊥ AH
c) ∆CHI vuông tại H
⇒ IC là cạnh huyền nên là cạnh lớn nhất
⇒ HI < IC
Mà HI = IA (cmt)
⇒ IA < IC
Đúng 1
Bình luận (0)