Question

Answer 1

Answer 2

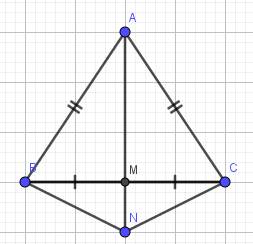
a) Do M là trung điểm của BC (gt)

⇒ BM = CM

Do ∆ABC cân tại A (gt)

⇒ AB = AC và ∠ABC = ∠ACB

Do ∠ABC = ∠ACB (cmt)

⇒ ∠ABM = ∠ACM

Xét ∆ABM và ∆ACM có:

AB = AC (cmt)

∠ABM = ∠ACM (cmt)

BM = CM (cmt)

⇒ ∆ABM = ∆ACM (c-g-c)

b) Do AB = AC (cmt)

⇒ A nằm trên đường trung trực của BC (1)

Do BM = CM (cmt)

⇒ M nằm trên đường trung trực của BC (2)

Từ (1) và (2) ⇒ AM là đường trung trực của BC

c) Do AM là đường trung trực của BC (cmt)

⇒ N nằm trên AM

⇒ NB = NC (tính chất đường trung trực của đoạn thẳng)

⇒ ∆NBC cân tại N

d) Xét ∆ABN và ∆ACN có:

AB = AC (cmt)

AN là cạnh chung

NB = NC (cmt)

⇒ ∆ABN = ∆ACN (c-c-c)

⇒ ∠ANB = ∠ANC (hai góc tương ứng)

⇒ NA là tia phân giác của ∠BNC