Question

  

Answer 1

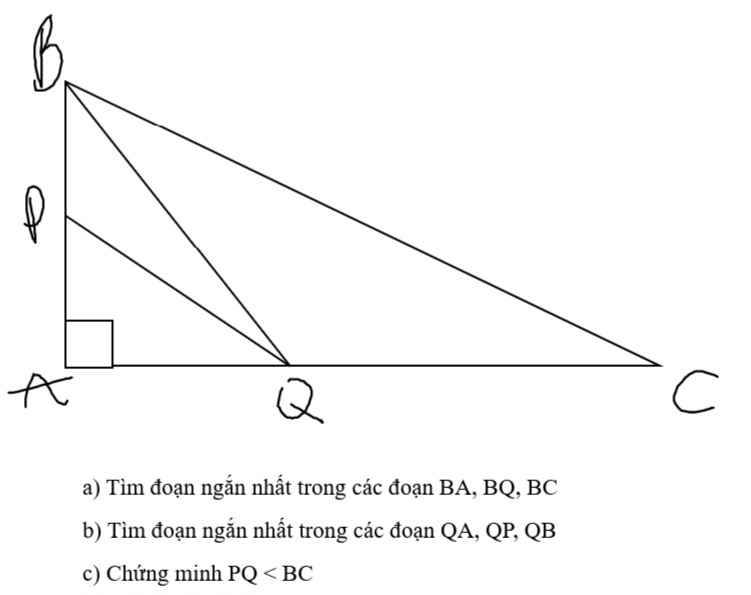
a: ΔBAQ vuông tại A

=>BA<BQ

Xét ΔBAQ có \(\widehat{BQC}\) là góc ngoài tại Q

nên \(\widehat{BQC}=\widehat{BAQ}+\widehat{ABQ}=90^0+\widehat{ABQ}>90^0\)

Xét ΔBQC có \(\widehat{BQC}>90^0\)

nên BC là cạnh lớn nhất trong ΔBQC

=>BQ<BC

=>BA<BQ<BC

c: Xét ΔAPQ có \(\widehat{BPQ}\) là góc ngoài tại P

nên \(\widehat{BPQ}=\widehat{PAQ}+\widehat{PQA}=90^0+\widehat{PQA}>90^0\)

Xét ΔBPQ có \(\widehat{BPQ}>90^0\)

nên BQ là cạnh lớn nhất trong ΔBPQ

=>BQ>PQ

mà BQ<BC

nên PQ<BC