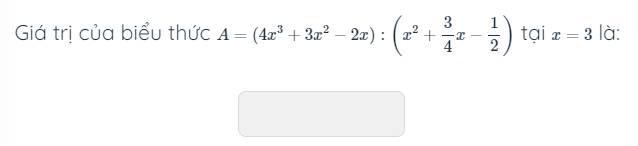1: \(\dfrac{20x^5-18x^4+6x^2-4x}{-2x}\)
\(=-\dfrac{20x^5}{2x}+\dfrac{18x^4}{2x}-\dfrac{6x^2}{2x}+\dfrac{4x}{2x}\)
\(=-10x^4+9x^3-3x+2\)
2: \(\dfrac{4x^4+3x^2-2x+1}{x^2+1}\)
\(=\dfrac{4x^4+4x^2-x^2-1-2x+2}{x^2+1}\)
\(=4x^2-1+\dfrac{-2x+2}{x^2+1}\)
=>Đa thức dư là -2x+2
3: \(A=\left(4x^3+3x^2-2x\right):\left(x^2+\dfrac{3}{4}x-\dfrac{1}{2}\right)\)
Thay x=3 vào A, ta được:
\(A=\dfrac{4\cdot3^3+3\cdot3^2-2\cdot3}{3^2+\dfrac{3}{4}\cdot3-\dfrac{1}{2}}=\dfrac{4\cdot27+27-6}{9+\dfrac{9}{4}-\dfrac{1}{2}}=12\)
4: \(15x^2-10x+a⋮5x-3\)
=>\(15x^2-9x-x+0,6+a-0,6⋮5x-3\)
=>a-0,6=0
=>a=0,6=3/5
5: \(x^3+ax^2-4⋮x^2+4x+4\)
=>\(x^3+4x^2+4x+\left(a-4\right)x^2+\left(4a-16\right)x+4a-16+\left(-4a+12\right)a-4a+12⋮x^2+4x+4\)
=>-4a+12=0
=>a=3
6: \(\dfrac{3x^3-2x^2+5}{3x-2}\)
\(=\dfrac{x^2\left(3x-2\right)+5}{3x-2}=x^2+\dfrac{5}{3x-2}\)
=>SAi