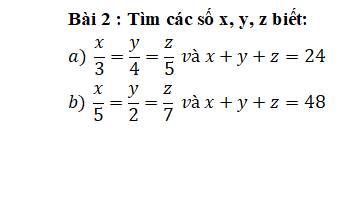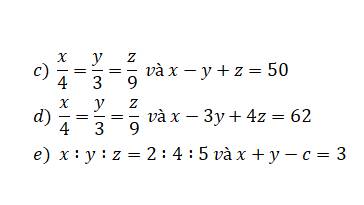a: \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
mà x+y+z=24
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{24}{12}=2\)
=>\(x=2\cdot3=6;y=2\cdot4=8;z=5\cdot2=10\)
b: \(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{7}\)
mà x+y+z=48
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{x+y+z}{5+2+7}=\dfrac{48}{14}=\dfrac{24}{7}\)
=>\(x=\dfrac{24}{7}\cdot5=\dfrac{120}{7};y=\dfrac{24}{7}\cdot2=\dfrac{48}{7};z=\dfrac{24}{7}\cdot7=24\)
c: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}\)
mà x-y+z=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}=\dfrac{x-y+z}{4-3+9}=\dfrac{50}{10}=5\)
=>\(x=4\cdot5=20;y=3\cdot5=15;z=9\cdot5=45\)
d: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}\)
mà x-3y+4z=62
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{9}=\dfrac{x-3y+4z}{4-3\cdot3+4\cdot9}=\dfrac{62}{31}=2\)
=>\(x=2\cdot4=8;y=2\cdot3=6;z=2\cdot9=18\)
e:
Sửa đề: x+y-z=3
x:y:z=2:4:5
=>\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}\)
mà x+y-z=3
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{2+4-5}=\dfrac{3}{1}=3\)
=>\(x=3\cdot2=6;y=3\cdot4=12;z=3\cdot5=15\)
\(a.\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}và+y+z=24\)
\(\Rightarrow\dfrac{x+y+z}{3+4+5++}=\dfrac{24}{12}=2\)
\(\dfrac{x}{3}=2\Rightarrow x=6\\ \dfrac{y}{4}=2\Rightarrow y=8\\ \dfrac{z}{5}=2\Rightarrow z=10\)