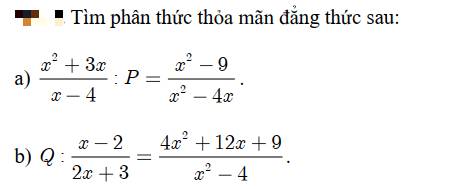a: ĐKXĐ: \(x\notin\left\{0;4;3;-3\right\}\)
\(\dfrac{x^2+3x}{x-4}:P=\dfrac{x^2-9}{x^2-4x}\)
=>\(P=\dfrac{x^2+3x}{x-4}:\dfrac{x^2-9}{x^2-4x}\)
\(=\dfrac{x\left(x+3\right)}{x-4}\cdot\dfrac{x\left(x-4\right)}{\left(x-3\right)\cdot\left(x+3\right)}\)
=>\(P=\dfrac{x^2}{x-3}\)
b: ĐKXĐ: \(x\notin\left\{2;-2;-\dfrac{3}{2}\right\}\)
\(Q:\dfrac{x-2}{2x+3}=\dfrac{4x^2+12x+9}{x^2-4}\)
=>\(Q=\dfrac{4x^2+12x+9}{x^2-4}\cdot\dfrac{x-2}{2x+3}\)
=>\(Q=\dfrac{\left(2x+3\right)^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x-2}{2x+3}\)
=>\(Q=\dfrac{2x+3}{x+2}\)
a) \(\dfrac{x^2+3x}{x-4}:P=\dfrac{x^2-9}{x^2-4x}\left(x\ne4;0;\pm3\right)\)
\(\Leftrightarrow P=\dfrac{x\left(x+3\right)}{x-4}:\dfrac{\left(x+3\right)\left(x-3\right)}{x\left(x-4\right)}\)
\(\Leftrightarrow P=\dfrac{x\left(x+3\right)}{x-4}\cdot\dfrac{x\left(x-4\right)}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow P=\dfrac{x^2}{x-3}\)
b) \(Q:\dfrac{x-2}{2x+3}=\dfrac{4x^2+12x+9}{x^2-4}\left(x\ne-\dfrac{3}{2};\pm2\right)\)
\(\Leftrightarrow Q=\dfrac{4x^2+12x+9}{x^2-4}\cdot\dfrac{x-2}{2x+3}\)
\(\Leftrightarrow Q=\dfrac{\left(2x+3\right)^2}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{x-2}{2x+3}\)
\(\Leftrightarrow Q=\dfrac{2x+3}{x+2}\)