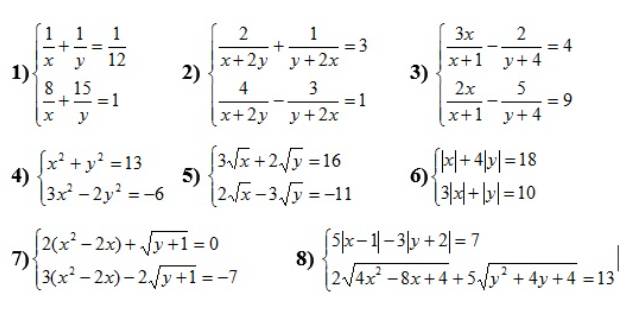1) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\left(x,y\ne0\right)\)
Đặt: \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=\dfrac{1}{12}\\8u+15v=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{1}{28}\\v=\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{28}\\\dfrac{1}{y}=\dfrac{1}{21}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=28\\y=21\end{matrix}\right.\left(tm\right)\)
1: ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=\dfrac{2}{3}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y}=\dfrac{1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=21\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{21}=\dfrac{1}{28}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=21\\x=28\end{matrix}\right.\left(nhận\right)\)
2: ĐKXĐ: x<>-2y và y<>-2x
\(\left\{{}\begin{matrix}\dfrac{2}{x+2y}+\dfrac{1}{2x+y}=3\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+2y}+\dfrac{3}{2x+y}=9\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x+2y}=10\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=1\\\dfrac{3}{2x+y}=4-1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\2x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=1\\x+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=1-2y=\dfrac{1}{3}\end{matrix}\right.\)(nhận)
3: ĐKXĐ: x<>-1 và y<>-4
\(\left\{{}\begin{matrix}\dfrac{3x}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3x+3-3}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3-\dfrac{3}{x+1}-\dfrac{2}{y+4}=4\\2-\dfrac{2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{x+1}+\dfrac{2}{y+4}=-1\\\dfrac{2}{x+1}+\dfrac{5}{y+4}=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+1}+\dfrac{4}{y+4}=-2\\\dfrac{6}{x+1}+\dfrac{15}{y+4}=-21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{11}{y+4}=19\\\dfrac{2}{x+1}+\dfrac{5}{y+4}=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y+4=-\dfrac{11}{19}\\\dfrac{2}{x+1}=-7-5:\dfrac{-11}{19}=\dfrac{18}{11}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{11}{19}-4=-\dfrac{11}{19}-\dfrac{76}{19}=-\dfrac{87}{19}\\x+1=\dfrac{22}{18}=\dfrac{11}{9}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{87}{19}\\x=\dfrac{2}{9}\end{matrix}\right.\left(nhận\right)\)
4: \(\left\{{}\begin{matrix}x^2+y^2=13\\3x^2-2y^2=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x^2+3y^2=39\\3x^2-2y^2=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y^2=45\\x^2+y^2=13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y^2=9\\x^2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in\left\{3;-3\right\}\\x\in\left\{2;-2\right\}\end{matrix}\right.\)
5:
ĐKXĐ: x>=0 và y>=0
\(\left\{{}\begin{matrix}3\sqrt{x}+2\sqrt{y}=16\\2\sqrt{x}-3\sqrt{y}=-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9\sqrt{x}+6\sqrt{y}=48\\4\sqrt{x}-6\sqrt{y}=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13\sqrt{x}=26\\3\sqrt{x}+2\sqrt{y}=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}=2\\2\sqrt{y}=16-6=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=25\end{matrix}\right.\left(nhận\right)\)
6: \(\left\{{}\begin{matrix}\left|x\right|+4\left|y\right|=18\\3\left|x\right|+\left|y\right|=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left|x\right|+12\left|y\right|=54\\3\left|x\right|+\left|y\right|=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left|y\right|=44\\\left|x\right|+4\left|y\right|=18\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left|y\right|=4\\\left|x\right|=18-16=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in\left\{4;-4\right\}\\x\in\left\{2;-2\right\}\end{matrix}\right.\)
7: ĐKXĐ: y>=-1
\(\left\{{}\begin{matrix}2\left(x^2-2x\right)+\sqrt{y+1}=0\\3\left(x^2-2x\right)-2\sqrt{y+1}=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(x^2-2x\right)+2\sqrt{y+1}=0\\3\left(x^2-2x\right)-2\sqrt{y+1}=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7\left(x^2-2x\right)=-7\\2\left(x^2-2x\right)+\sqrt{y+1}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-2x=-1\\\sqrt{y+1}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-2x+1=0\\y+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=0\\y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\left(nhận\right)\)
8: \(\left\{{}\begin{matrix}5\left|x-1\right|-3\left|y+2\right|=7\\2\sqrt{4x^2-8x+4}+5\sqrt{y^2+4y+4}=13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5\left|x-1\right|-3\left|y+2\right|=7\\2\cdot2\sqrt{\left(x-1\right)^2}+5\cdot\sqrt{\left(y+2\right)^2}=13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5\left|x-1\right|-3\left|y+2\right|=7\\4\left|x-1\right|+5\left|y+2\right|=13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}25\left|x-1\right|-15\left|y+2\right|=35\\12\left|x-1\right|+15\left|y+2\right|=39\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}37\left|x-1\right|=74\\4\left|x-1\right|+5\left|y+2\right|=13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left|x-1\right|=2\\5\left|y+2\right|=13-4\cdot2=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left|x-1\right|=2\\\left|y+2\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1\in\left\{2;-2\right\}\\y+2\in\left\{1;-1\right\}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{3;-1\right\}\\y\in\left\{-1;-3\right\}\end{matrix}\right.\)