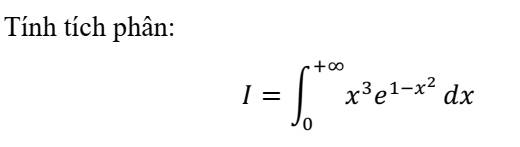Trước hết tính nguyên hàm:
\(J=\int x^3e^{1-x^2}dx\)
Đặt \(\left\{{}\begin{matrix}u=x^2\\dv=x.e^{1-x^2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=-\dfrac{1}{2}e^{1-x^2}\end{matrix}\right.\)
\(\Rightarrow J=-\dfrac{1}{2}e^{1-x^2}.x^2+\int x.e^{1-x^2}dx=-\dfrac{1}{2}e^{1-x^2}.x^2-\dfrac{1}{2}e^{1-x^2}+C=-\dfrac{1}{2}e^{1-x^2}\left(x^2+1\right)+C\)
\(\Rightarrow I=\lim\limits_{a\rightarrow+\infty}\left(-\dfrac{1}{2}e^{1-x^2}.\left(x^2+1\right)\right)|^a_0=\lim\limits_{a\rightarrow+\infty}\left(-\dfrac{1}{2}e^{1-a^2}\left(a^2+1\right)+\dfrac{1}{2}e\right)\)
\(=\dfrac{1}{2}e-\dfrac{1}{2}\lim\limits_{a\rightarrow+\infty}\dfrac{a^2+1}{e^{a^2-1}}=\dfrac{1}{2}e-\dfrac{1}{2}\lim\limits_{a\rightarrow+\infty}\dfrac{2a}{2a.e^{a^2-1}}\)
\(=\dfrac{1}{2}e-\dfrac{1}{2}\lim\limits_{a\rightarrow+\infty}\dfrac{1}{e^{a^2-1}}=\dfrac{1}{2}e-0=\dfrac{1}{2}e\)