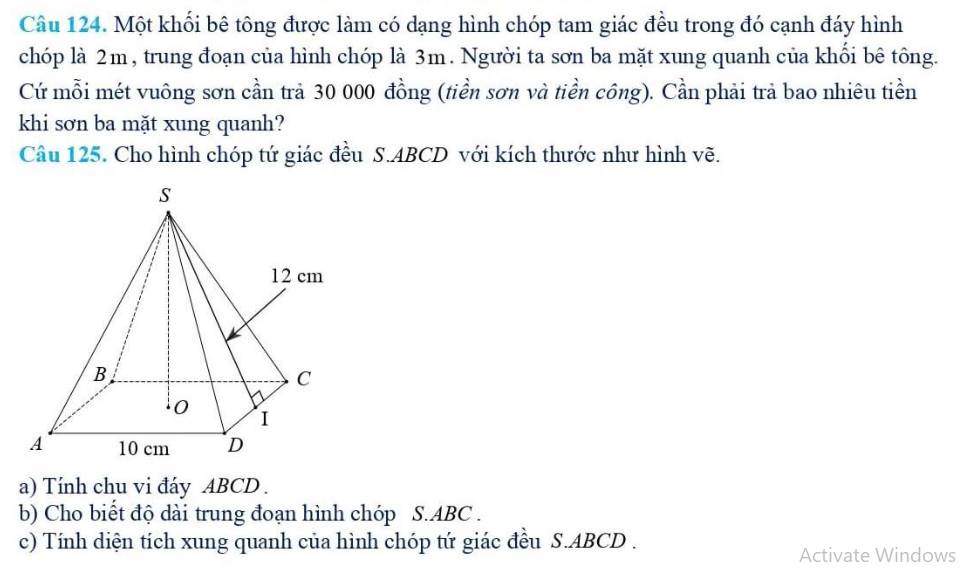
125:
a: Chu vi đáy ABCD là:
10*4=40(cm)
b:
Sửa đề: Tính trung đoạn của hình chóp S.ABCD
S.ABCD là hình chóp tứ giác đều
=>SA=SB=SC=SD
=>ΔSCD cân tại S
ΔSCD cân tại S
mà SI là đường cao
nên I là trung điểm của CD
=>\(IC=ID=\dfrac{DC}{2}=5\left(cm\right)\)
ΔSID vuông tại I
=>\(SI^2+ID^2=SD^2\)
=>\(SD^2=5^2+12^2=169\)
=>SD=13(cm)
=>SA=SB=SC=SD=13(cm)
ABCD là hình vuông
=>\(AC^2=AB^2+BC^2\)
=>\(AC^2=10^2+10^2=200\)
=>\(AC=10\sqrt{2}\left(cm\right)\)
ABCD là hình vuông có O là tâm
nên \(AO=BO=CO=DO=\dfrac{AC}{2}=\dfrac{10\sqrt{2}}{2}=5\sqrt{2}\left(cm\right)\)
S.ABCD là hình chóp tứ giác đều có O là tâm của đáy ABCD
=>SO là trung đoạn của hình chóp S.ABCD
=>SO\(\perp\)(ABCD)
=>SO\(\perp\)DO
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2+\left(5\sqrt{2}\right)^2=13^2\)
=>\(SO^2+50=169\)
=>\(SO^2=119\)
=>\(SO=\sqrt{119}\left(cm\right)\)
c: Diện tích xung quanh của hình chóp S.ABCD là:
\(S_{Xq}=C_{Đáy}\cdot SO=\sqrt{119}\cdot40\left(cm^2\right)\)