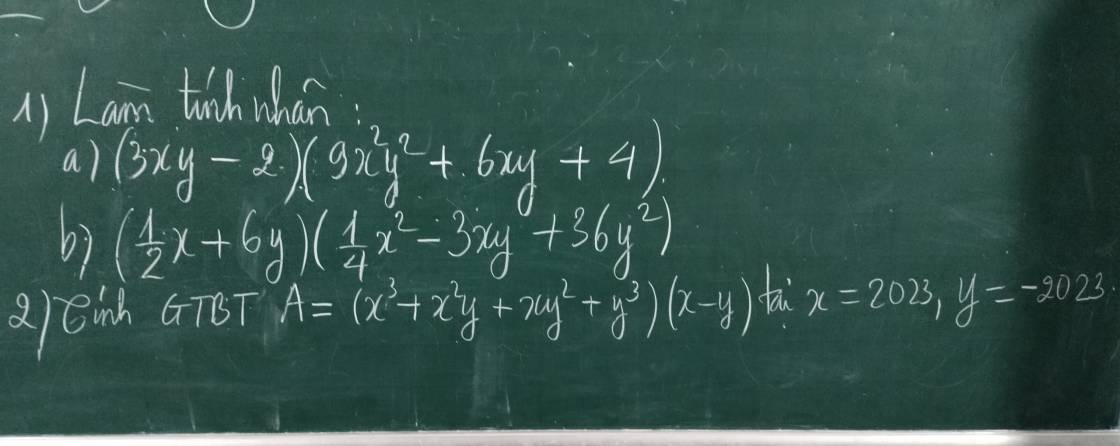1)
a)
\(\left(3xy-2\right)\left(9x^2y^2+6xy+4\right)\\ =\left(3xy-2\right)\left(\left(3xy\right)^2+3xy.2+2^2\right)\\ =\left(3xy\right)^3-2^3\\ =27x^3y^3-8\)
b)
\(\left(\dfrac{1}{2}x+6y\right)\left(\dfrac{1}{4}x^2-3xy+36y^2\right)\\ =\left(\dfrac{1}{2}x+6y\right)\left(\left(\dfrac{1}{2}x\right)^2-\dfrac{1}{2}x.6y+\left(6y\right)^2\right)\\ =\left(\dfrac{1}{2}x\right)^3+\left(6y\right)^3\\ =\dfrac{1}{8}x^3+216y^3\)
1)
a) (3xy - 2)(9x²y² + 6xy + 4)
= 27x³y³ + 18x²y² + 12xy - 18x²y² - 12xy - 8
= 26x³y³ + (18x²y² - 18x²y²) + (12xy - 12xy) - 8
= 27x³y³ - 8
b) (1/2 x + 6y)(1/4 x² - 3xy + 36y²)
= x³/8 - 3x²y/2 + 18xy² + 3x²y/2 - 18xy² + 216y³
= x³/8 + (-3x²y/2 + 3x²y/2) + (18xy² - 18xy²) + 216y³
= x³/8 + 216y³
2) A = (x³ + x²y + xy² + y³)(x - y)
= x⁴ - x³y + x³y - x²y² + x²y² - xy³ + xy³ - y⁴
= x⁴ + (-x³y + x³y) + (-x²y² + x²y²) + (-xy³ + xy³) - y⁴
= x⁴ - y⁴
Thay x = 2023; y = 2023 vào A, ta được:
A = 2023⁴ - 2023⁴
= 0