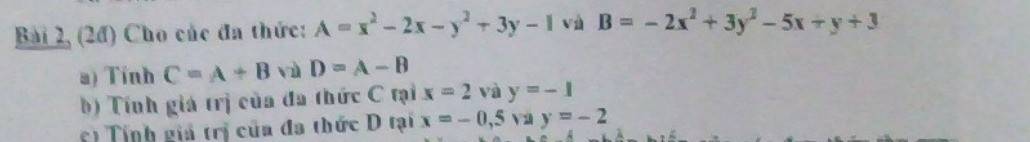a) \(C=A+B\)
\(C=\left(x^2-2x-y^2+3y-1\right)+\left(-2x^2+3y^2-5x+y+3\right)\)
\(C=x^2-2x-y^2+3y-1-2x^2+3y^2-5x+y+3\)
\(C=\left(x^2-2x^2\right)-\left(2x+5x\right)-\left(y^2-3y^2\right)+\left(3y+y\right)-\left(1-3\right)\)
\(C=-x^2-7x+2y^2+4y+2\)
\(D=A-B\)
\(D=\left(x^2-2x-y^2+3y-1\right)-\left(-2x^2+3y^2-5x+y+3\right)\)
\(D=x^2-2x-y^2+3y-1+2x^2-3y^2+5x-y-3\)
\(D=\left(x^2+2x^2\right)-\left(2x-5x\right)-\left(y^2+3y^2\right)+\left(3y-y\right)-\left(1+3\right)\)
\(D=3x^2+3x-4y^2+2y-4\)
b) Thay x=2 và y=-1 vào C ta có:
\(C=-2^2-7\cdot2+2\cdot\left(-1\right)^2+4\cdot-1+2=-18\)
c) Thay x=-0,5 và y=-2 ta có:
\(D=3\cdot\left(-0,5\right)^2+3\cdot-0,5-4\cdot\left(-2\right)^2+2\cdot-2-4=-24,75\)
\(a,A=x^2-2x-y^2+3y-1\)
\(B=-2x^2+3y^2-5x+y+3\)
\(C=A+B\)
\(=x^2-2x-y^2+3y-1+\left(-2x^2\right)+3y^2-5x+y+3\)
\(=\left(x^2-2x^2\right)+\left(-y^2+3y^2\right)+\left(-2x-5x\right)+\left(3y+y\right)+\left(-1+3\right)\)
\(=-x^2+2y^2-7x+4y+2\)
\(D=A-B\)
\(=x^2-2x-y^2+3y-1-\left(-2x^2+3y^2-5x+y+3\right)\)
\(=x^2-2x-y^2+3y-1+2x^2-3y^2+5x-y-3\)
\(=\left(x^2+2x^2\right)+\left(-y^2-3y^2\right)+\left(-2x+5x\right)+\left(3y-y\right)+\left(-1-3\right)\)
\(=3x^2-4y^2+3x+2y-4\)
\(b,C=-x^2+2y^2-7x+4y+2\)
Thay \(x=2;y=-1\) vào C, ta được:
\(C=-2^2+2\cdot\left(-1\right)^2-7\cdot2+4\cdot\left(-1\right)+2\)
\(=-4+2-14-4+2\)
\(=\left(-4+2\right)+\left(-14-4\right)+2\)
\(=-2-18+2\)
\(=-18\)
\(c,D=3x^2-4y^2+3x+2y-4\)
Thay \(x=-0,5;y=-2\) vào D, ta được:
\(D=3\cdot\left(-0,5\right)^2-4\cdot\left(-2\right)^2+3\cdot\left(-0,5\right)+2\cdot\left(-2\right)-4\)
\(=3\cdot0,25-4\cdot4-1,5-4-4\)
\(=0,75-16-1,5-8\)
\(=\left(0,75-1,5\right)-\left(16+8\right)\)
\(=-0,75-24\)
\(=-24,75\)
#\(Urushi\)