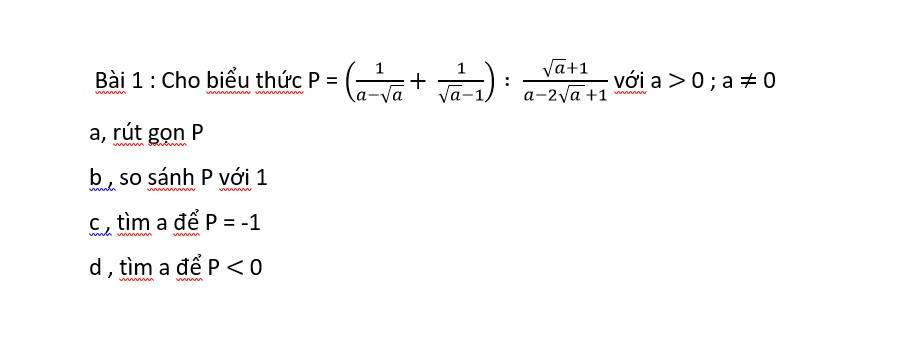a.
\(P=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{\sqrt{a}}{a-\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\right)\\ =\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}+1}\\ =\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b.
\(1=\dfrac{\sqrt{a}}{\sqrt{a}}\\ \Rightarrow\dfrac{\sqrt{a}-1}{\sqrt{a}}< 1\)
c.
\(P=-1\\ \Leftrightarrow\dfrac{\sqrt{a}-1}{\sqrt{a}}=-1\\ \Leftrightarrow-\sqrt{a}-\sqrt{a}+1=0\\ \Leftrightarrow1-2\sqrt{a}=0\\ \Leftrightarrow2\sqrt{a}=1\\ \Leftrightarrow\sqrt{a}=\dfrac{1}{2}\\ \Leftrightarrow a=\dfrac{1}{4}\left(tmđk\right)\)
Vậy để `P=-1` thì `a=1/4`
d.
\(P< 0\\ \Leftrightarrow\dfrac{\sqrt{a}-1}{\sqrt{a}}< 0\\ \Leftrightarrow\sqrt{a}-1< 0\left(do.a>0\right)\\ \Leftrightarrow\sqrt{a}< 1\\ \Leftrightarrow a< 1\)
Kết hợp điều kiện `a>0`, kết luận: để `P<0` thì \(0< a< 1\)
\(P =\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\) (ĐKXĐ: a > 0; a ≠ 0)
\(=\left(\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\)
\(=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
\(b,P=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
\(1=\dfrac{\sqrt{a}}{\sqrt{a}}\)
\(\Rightarrow P< 1\)
\(c,P=\dfrac{\sqrt{a}-1}{\sqrt{a}}=-1\)
\(\Leftrightarrow\sqrt{a}-1=-\sqrt{a}\)
\(\Leftrightarrow2\sqrt{a}=1\Leftrightarrow\sqrt{a}=\dfrac{1}{2}\)
\(\Leftrightarrow a=\dfrac{1}{4}\)(tmđk)
\(d,P=\dfrac{\sqrt{a}-1}{\sqrt{a}}< 0\)
\(\Leftrightarrow\sqrt{a}-1< 0\)
\(\Leftrightarrow\sqrt{a}< 1\Leftrightarrow0< a< 1\) (đb)