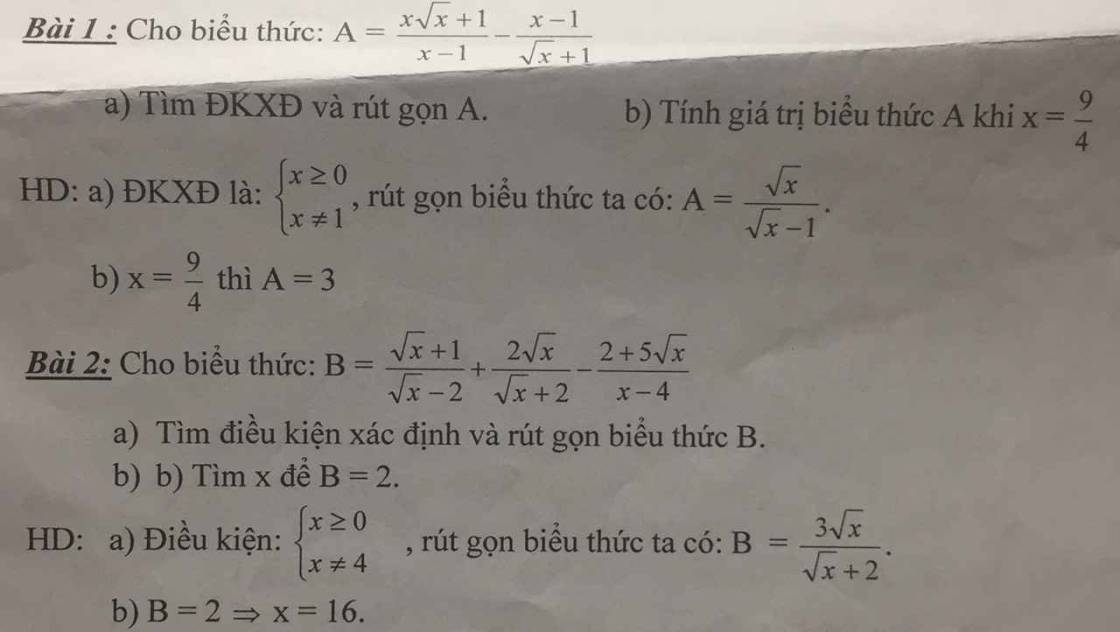Bài 1:
a) ĐKXĐ: \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\x-1\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(A=\dfrac{x\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Thay \(x=\dfrac{9}{4}\) vào A ta có:
\(A=\dfrac{\sqrt{\dfrac{9}{4}}}{\sqrt{\dfrac{9}{4}}-1}=\dfrac{\dfrac{3}{2}}{\dfrac{3}{2}-1}=3\)
Vậy: ....
2:
a: ĐKXĐ: x>=0; x<>4
\(B=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{x-4}=\dfrac{3x-6\sqrt{x}}{x-4}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b: B=2
=>3căn x=2căn x+4
=>căn x=4
=>x=16