`2,`
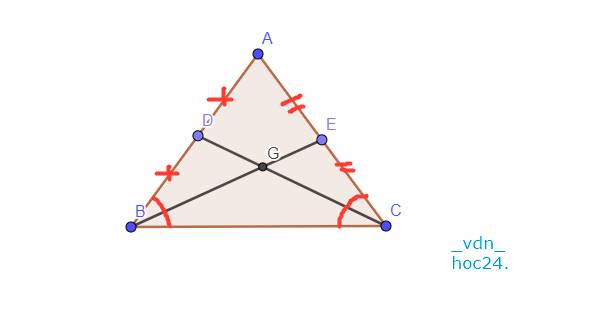
`BE, CD` là đường trung tuyến.
Giả sử \(BE\cap CD=G\)
`-> G` là trọng tâm của Tam giác `ABC`
`-> GB=2/3 BE , GC=2/3 CD`
`BE = CD -> GB = GC`
`->` \(\text{Tam giác GBC cân tại G}\)`.`
`->`\(\widehat{B_1}=\widehat{C_1}\)
Xét Tam giác `BEC` và Tam giác `CDB` có:
\(\left\{{}\begin{matrix}BE=CD\left(gt\right)\\\widehat{B_1}=\widehat{C_1}\left(CMT\right)\\BC\text{ chung}\end{matrix}\right.\)
`=> \text {Tam giác BEC = Tam giác CDB (c-g-c)}`
`-> BD=CE (\text {2 cạnh tương ứng})`
`-> 1/2 AB = 1/2 AC`
`-> AB = AC`
`-> \text {Tam giác ABC cân tại A (đpcm}.`
`3,`
`BE` là đường trung tuyến
`->` \(\text{E là trung điểm của AC}\)
`-> \text {AE = EC}`
`CD` là đường trung tuyến
`->` \(\text{D là trung điểm của AB}\)
`->`\(\text{ DA = DB}\)
Xét Tam giác `ABC` cân tại `A`
`-> AB = AC`
` -> AE=AD=DB=EC`
Xét Tam giác `BEC` và Tam giác `CDB` có:
`DB = EC (CMT)`
\(\widehat{B}=\widehat{C} (\text {Tam giác ABC cân tại A})\)
`\text {BC chung}`
`=> \text {Tam giác BEC = Tam giác CDB (c-g-c)}`
`=> BE = CD (\text {2 cạnh tương ứng}) (đpcm)`
B2:

B3:
3:
Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD



