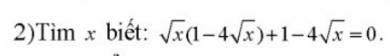\(\sqrt{x}\) ( 1 - 4\(\sqrt{x}\)) + 1 - 4\(\sqrt{x}\) = 0 ( đk \(x\ge0\))
( 1 - 4\(\sqrt{x}\))( \(\sqrt{x}\) + 1) = 0
vì \(\sqrt{x}\) \(\ge\) 0 \(\Rightarrow\) \(\sqrt{x}\)+ 1 \(\ge\)1
\(\Rightarrow\) ( 1-4\(\sqrt{x}\) )(\(\sqrt{x}\) + 1) = 0 \(\Leftrightarrow\) 1 - 4\(\sqrt{x}\) = 0 => \(\sqrt{x}\) = 1/4 \(\Rightarrow\)x = 1/16 (tm)
Kết luận : \(x\) = \(\dfrac{1}{16}\)
ĐKXĐ: \(x\ge0\)
\(\sqrt{x}\left(1-4\sqrt{x}\right)+1-4\sqrt{x}=0\)
\(\left(1-4\sqrt{x}\right)\left(\sqrt{x}+1\right)=0\)
\(1-4\sqrt{x}=0\) hoặc \(\sqrt{x}+1=0\)
*) \(1-4\sqrt{x}=0\)
\(4\sqrt{x}=1\)
\(\sqrt{x}=\dfrac{1}{4}\)
\(x=\dfrac{1}{16}\) (nhận)
*) \(\sqrt{x}+1=0\)
\(\sqrt{x}=-1\) (vô lý)
Vậy \(x=\dfrac{1}{16}\)
ĐKXĐ: \(x\ge0\)
\(\sqrt{x}\left(1-4\sqrt{x}\right)+1-4\sqrt{x}=0\)
\(\left(1-4\sqrt{x}\right)\left(\sqrt{x}+1\right)=0\)
\(1-4\sqrt{x}=0\) hoặc \(\sqrt{x}+1=0\)
*) \(1-4\sqrt{x}=0\)
\(4\sqrt{x}=1\)
\(\sqrt{x}=\dfrac{1}{4}\)
\(x=\dfrac{1}{16}\) (nhận)
*) \(\sqrt{x}+1=0\)
\(\sqrt{x}=-1\) (vô lý)
Vậy \(x=\dfrac{1}{16}\)