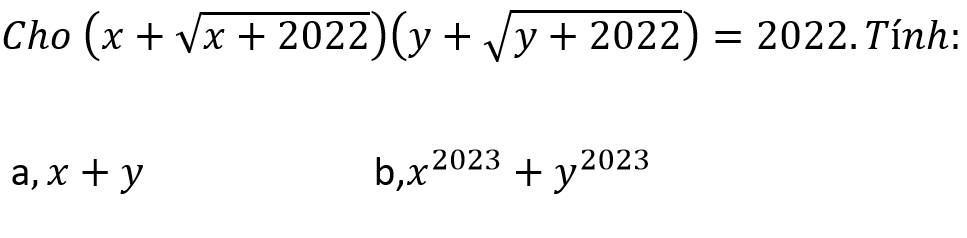a: Sửa đề: \(\left(x+\sqrt{x^2+2022}\right)\left(y+\sqrt{y^2+2022}\right)=2022\)
\(\Leftrightarrow\left(x+\sqrt{x^2+2022}\right)\left(x-\sqrt{x^2+2022}\right)\left(y+\sqrt{y^2+2022}\right)=2022\left(x-\sqrt{x^2+2022}\right)\)
=>\(-2022\left(y+\sqrt{y^2+2022}\right)=2022\left(x-\sqrt{x^2+2022}\right)\)
=>\(y+\sqrt{y^2+2022}=-x+\sqrt{x^2+2022}\)(1)
\(\left(x+\sqrt{x^2+2022}\right)\left(y+\sqrt{y^2+2022}\right)=2022\)
=>\(\left(x+\sqrt{x^2+2022}\right)\left(y+\sqrt{y^2+2022}\right)\left(y-\sqrt{y^2+2022}\right)=2022\left(y-\sqrt{y^2+2022}\right)\)
=>\(x+\sqrt{x^2+2022}=-y+\sqrt{y^2+2022}\)(2)
Từ (1), (2) suy ra x=-y
=>x+y=0
b: x^2023+y^2023
=x^2023+(-x)^2023
=0
Đúng 0
Bình luận (0)