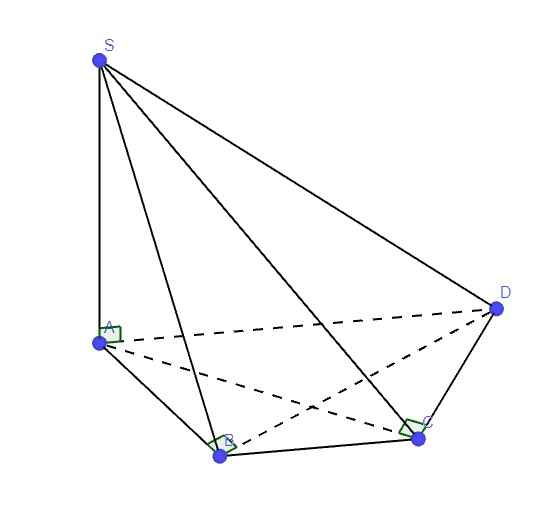
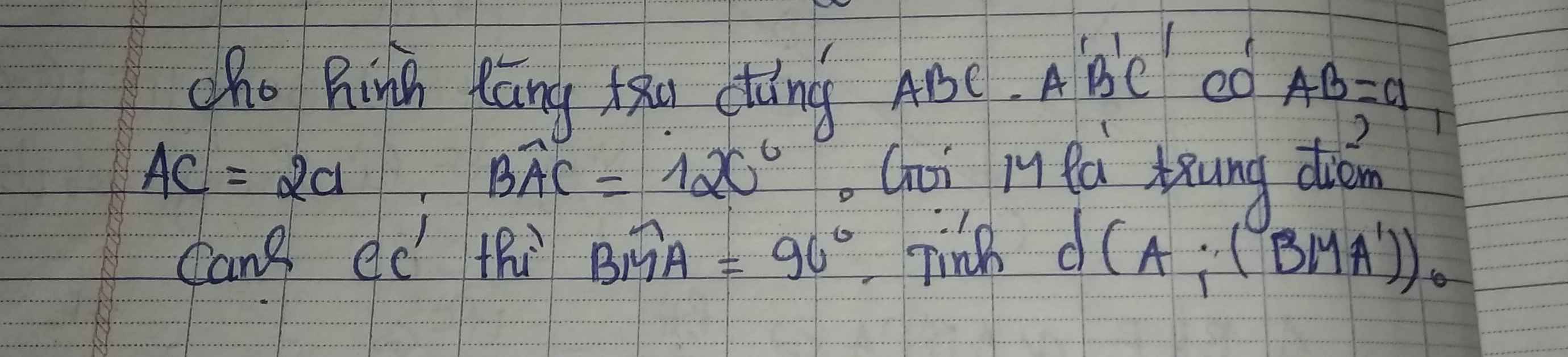Do ABCD là nửa lục giác đều đường kính AD \(\Rightarrow AC\perp CD\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAC\right)\)
\(\Rightarrow SC\) là hình chiếu vuông góc của SD lên (SAC)
Hay \(\widehat{CSD}\) là góc giữa SD và (SAC)
\(CD=\dfrac{1}{2}AD=a\) ; \(SD=\sqrt{SA^2+AD^2}=2a\sqrt{2}\)
\(\Rightarrow sin\widehat{CSD}=\dfrac{CD}{SD}=\dfrac{1}{2\sqrt{2}}\Rightarrow\widehat{CSD}\approx20^042'\)
b.
Do ABCD là nửa lục giác đều \(\Rightarrow BD\perp AB\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(\Rightarrow BD\perp\left(SAB\right)\Rightarrow SB\) là hình chiếu vuông góc của SD lên (SAB)
Hay \(\widehat{BSD}\) là góc giữa SD và (SAB)
\(AB=\dfrac{1}{2}AD=a\Rightarrow SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\)
\(\Rightarrow cos\widehat{BSD}=\dfrac{SB}{SD}=\dfrac{\sqrt{5}}{2\sqrt{2}}\Rightarrow\widehat{BSD}\approx37^046'\)