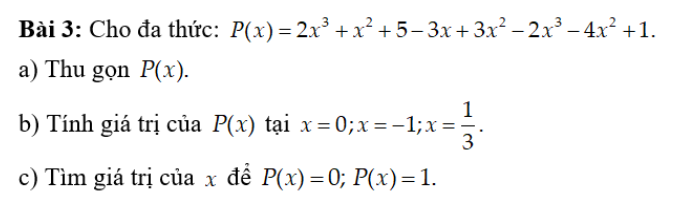Question

Answer 1

a: \(P\left(x\right)=\left(2x^3-2x^3\right)+\left(x^2+3x^2-4x^2\right)+\left(-3x\right)+5+1=-3x+6\)

b: P(0)=6

P(-1)=9

P(1/3)=-1+6=5

c: Để P(x)=0 thì -3x+6=0

hay x=2

để P(x)=1 thì -3x+6=1

=>-3x=-7

hay x=7/3

Answer 2

a.\(P\left(x\right)=-3x+6\)

b.

\(P\left(0\right)=-3.0+6=6\)

\(P\left(-1\right)=-3.-1+6=3+6=9\)

\(P\left(\dfrac{1}{3}\right)=-3.\dfrac{1}{3}+6=-1+6=5\)

c.

*\(P\left(x\right)=0\)

\(\Rightarrow-3x+6=0\)

\(-3x=-6\)

\(x=2\)

*\(P\left(x\right)=1\)

\(\Rightarrow-3x+6=1\)

\(-3x=-7\)

\(x=\dfrac{7}{3}\)

Answer 3

a. P(x) = 2x³ + x² + 5 - 3x +3x - 2x³ - 4x² + 1

        = (2x³ - 2x³ ) + (-4x² + x²) + (-3x + 3x) + 5 + 1

        =       0           -        3x²      +      0         +   6

        =       -3x²     +    6

b.+) Nếu x = 0 thì

 P(0) = -3 . 0²    +   6

        =  -3 . 0   + 6 

         =    0  +  6   = 6

+) Nếu x = -1 thì

P(-1) = -3 . (-1)²    +   6 

         =    -3     +     6  = 3

+)  Nếu x = \(\dfrac{1}{3}\) thì:

 P(\(\dfrac{1}{3}\)) = -3 . \(\left(\dfrac{1}{3}\right)\)²    +   6

         =   -3  .   \(\dfrac{1}{9}\)      +   6

         =     \(\dfrac{-1}{3}+\dfrac{18}{3}\) =   \(\dfrac{17}{3}\)