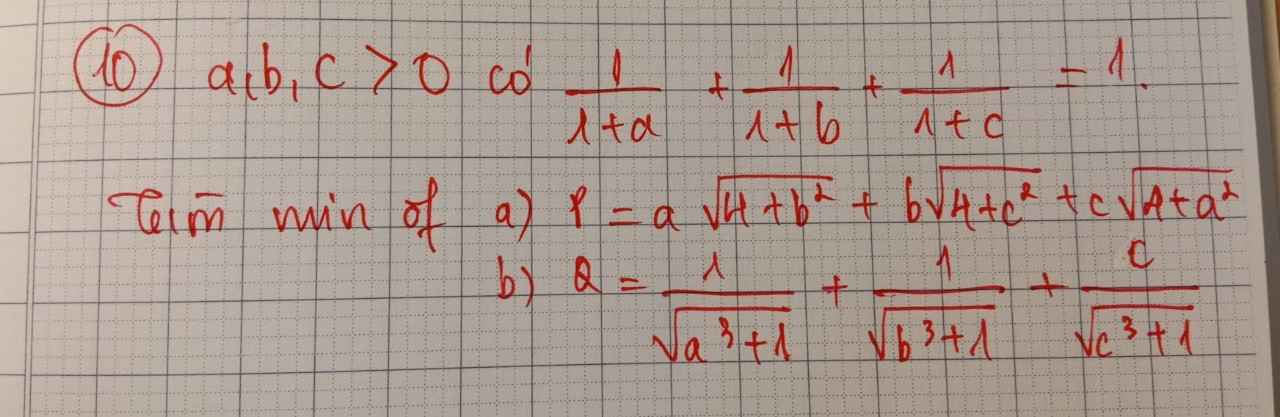\(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}=1\)
\(\Rightarrow\dfrac{a}{a+1}=\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge2\sqrt{\dfrac{1}{\left(b+1\right)\left(c+1\right)}}\)
Tương tự: \(\dfrac{b}{b+1}\ge2\sqrt{\dfrac{1}{\left(a+1\right)\left(c+1\right)}}\) ; \(\dfrac{c}{c+1}\ge2\sqrt{\dfrac{1}{\left(a+1\right)\left(b+1\right)}}\)
Nhân vế:
\(\dfrac{abc}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{8}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\)
\(\Rightarrow abc\ge8\)
a.
\(P=a\sqrt{4+b^2}+b\sqrt{4+c^2}+c\sqrt{4+a^2}\)
(Áp dụng \(4+x^2\ge\dfrac{1}{2}\left(2+x\right)^2\))
\(P\ge\dfrac{a}{\sqrt{2}}\left(2+b\right)+\dfrac{b}{\sqrt{2}}\left(2+c\right)+\dfrac{c}{\sqrt{2}}\left(2+a\right)\)
\(P\ge\dfrac{1}{\sqrt{2}}\left(2a+2b+2c+ab+bc+ca\right)\ge\dfrac{1}{\sqrt{2}}.\left(2.3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\right)\ge12\sqrt{2}\)
Dấu "=" xảy ra khi \(a=b=c=2\)
b.
\(\dfrac{1}{\sqrt{a^3+1}}=\dfrac{1}{\sqrt{\left(a+1\right)\left(a^2-a+1\right)}}\ge\dfrac{2}{a+1+a^2-a+1}=\dfrac{2}{a^2+2}\)
Tương tự: \(\dfrac{1}{\sqrt{b^3+1}}\ge\dfrac{2}{b^2+2}\) ; \(\dfrac{1}{\sqrt{c^3+1}}\ge\dfrac{2}{c^2+2}\)
\(\Rightarrow Q\ge\dfrac{2}{a^2+2}+\dfrac{2}{b^2+2}+\dfrac{2}{c^2+2}\)
Từ điều kiện ban đầu \(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}=1\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{1+a}=x\\\dfrac{1}{1+b}=y\\\dfrac{1}{1+c}=z\end{matrix}\right.\) \(\Rightarrow x+y+z=1\)
Đồng thời: \(\dfrac{1}{1+a}=x\Rightarrow1+a=\dfrac{1}{x}=\dfrac{x+y+z}{x}\Rightarrow a=\dfrac{x+y+z}{x}-1=\dfrac{y+z}{x}\)
Tương tự: \(b=\dfrac{z+x}{y}\) ; \(c=\dfrac{x+y}{z}\)
Từ đó:
\(Q\ge\dfrac{2}{\left(\dfrac{y+z}{x}\right)^2+2}+\dfrac{2}{\left(\dfrac{z+x}{y}\right)^2+2}+\dfrac{2}{\left(\dfrac{x+y}{z}\right)^2+2}\)
\(Q\ge\dfrac{2x^2}{2x^2+\left(y+z\right)^2}+\dfrac{2y^2}{2y^2+\left(z+x\right)^2}+\dfrac{2z^2}{2z^2+\left(x+y\right)^2}\)
\(Q\ge\dfrac{2x^2}{2x^2+2\left(y^2+z^2\right)}+\dfrac{2y^2}{2y^2+2\left(z^2+x^2\right)}+\dfrac{2z^2}{2z^2+2\left(x^2+y^2\right)}=1\)
\(Q_{min}=1\) khi \(x=y=z\) hay \(a=b=c=2\)