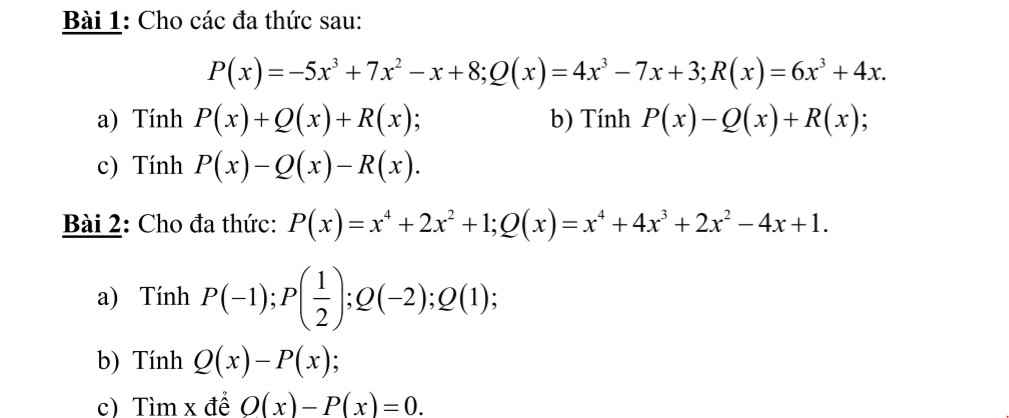Bài 2:
a: \(P\left(x\right)=x^4+2x^2+1=x^4+2\cdot x^2\cdot1+1^2=\left(x^2+1\right)^2\)
\(P\left(-1\right)=\left[\left(-1\right)^2+1\right]^2=\left[1+1\right]^2=4\)
\(P\left(\dfrac{1}{2}\right)=\left[\left(\dfrac{1}{2}\right)^2+1\right]^2=\left(\dfrac{1}{4}+1\right)^2=\left(\dfrac{5}{4}\right)^2=\dfrac{25}{16}\)
\(Q\left(x\right)=x^4+4x^3+2x^2-4x+1\)
\(Q\left(-2\right)=\left(-2\right)^4+4\cdot\left(-2\right)^3+2\cdot\left(-2\right)^2-4\cdot\left(-2\right)+1\)
\(=16+4\cdot\left(-8\right)+2\cdot4+8+1\)
\(=1\)
\(Q\left(1\right)=1^4+4\cdot1^3+2\cdot1^2-4\cdot1+1\)
\(=1+4+2-4+1\)
=1+2+1
=4
b: Q(x)-P(x)
\(=x^4+4x^3+2x^2-4x+1-x^4-2x^2-1\)
\(=4x^3-4x\)
c: Q(x)-P(x)=0
=>\(4x^3-4x=0\)
=>\(x^3-x=0\)
=>\(x\left(x^2-1\right)=0\)
=>\(x\left(x-1\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Bài 1:
a: P(x)+Q(x)+R(x)
\(=-5x^3+7x^2-x+8+4x^3-7x+3+6x^3+4x\)
\(=5x^3+7x^2-4x+11\)
b: P(x)-Q(x)+R(x)
\(=-5x^3+7x^2-x+8-4x^3+7x-3+6x^3+4x\)
\(=-3x^3+7x^2+10x+5\)
c: P(x)-Q(x)-R(x)
\(=-5x^3+7x^2-x+8-4x^3+7x-3-6x^3-4x\)
\(=-15x^3+7x^2+2x+5\)