a.
\(AB\perp\left(BCD\right)\Rightarrow BC\) là hình chiếu vuông góc của AC lên (BCD)
\(\Rightarrow\widehat{ACB}\) là góc giữa AC và (BCD)
\(tan\widehat{ACB}=\dfrac{AB}{BC}=\sqrt{3}\Rightarrow\widehat{ACB}=60^0\)
b.
Tương tự câu a, ta có BD là hình chiếu vuông góc của AD lên (BCD)
\(\Rightarrow\widehat{ADB}\) là góc giữa AD và (BCD)
\(tan\widehat{ADB}=\dfrac{AB}{AD}=\sqrt{3}\Rightarrow\widehat{ADB}=60^0\)
c.
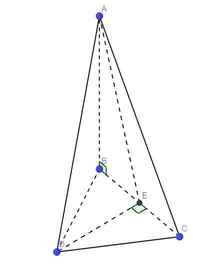
Gọi E là trung điểm BC \(\Rightarrow DE\perp BC\) (do BCD đều)
Mà \(AB\perp\left(BCD\right)\Rightarrow AB\perp DE\)
\(\Rightarrow DE\perp\left(ABC\right)\)
\(\Rightarrow AE\) là hình chiếu vuông góc của AD lên (ABC)
\(\Rightarrow\widehat{DAE}\) là góc giữa AD và (ABC)
\(DE=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(BE=\dfrac{1}{2}BC=\dfrac{a}{2}\Rightarrow AE=\sqrt{AB^2+BE^2}=\dfrac{a\sqrt[]{13}}{2}\)
\(\Rightarrow tan\widehat{DAE}=\dfrac{DE}{AE}=\dfrac{\sqrt{39}}{13}\Rightarrow\widehat{DAE}\approx25^039'\)